| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- airflow
- 표준편차
- sql
- 자연어 논문 리뷰
- GRU
- t분포
- inner join
- NLP
- 코딩테스트
- Window Function
- 논문리뷰
- leetcode
- nlp논문
- 설명의무
- CASE
- SQL코테
- 카이제곱분포
- 그룹바이
- MySQL
- 자연어 논문
- HackerRank
- update
- sigmoid
- SQL 날짜 데이터
- Statistics
- 서브쿼리
- 짝수
- torch
- LSTM
- 자연어처리
- Today
- Total
HAZEL
[Basic Statistics : CH 2. 데이터와 통계량] 데이터의 수집(척도), 데이터의 표현방법, 기초 통계량 본문
[Basic Statistics : CH 2. 데이터와 통계량] 데이터의 수집(척도), 데이터의 표현방법, 기초 통계량
Rmsid01 2020. 11. 6. 11:22CH2. 데이터와 통계량
01 . 데이터의 수집
001. 용어
- 변수 : 어떠한 대응관계로 변화하는 수, 혹은 함수관계로 대응하며 주어진 범위 안에서 변화하는 수
-> 변수는 데이터로 구성되고, 데이터를 근거로 변수의 특성을 파악
- 데이터 : 조사의 목적에 맞는 변수를 기반으로, 표본으로부터 수집된 자료
002. 척도 [ 적절한 데이터를 구성하기 위한 기준 ]
1. 범주형 척도 : 명목척도, 서열척도
: 하나하나 구분이 되어있는것
- 명목 척도 : 이름이나 명칭을 숫자를 부여하지만 수치에 의미가 없음
ex, 남 1 / 여 0 -> 남자와 1 / 여자와 0 은 서로 관계가 없음
- 서열 척도 ( 순서 척도 ) : 명목척도의 특징을 가지고 있으면서, 순서를 가짐 ex, 1등 2등 ,,
2. 연속형 척도 : 등간척도, 비율척도
: 구분이 되어있지 않고, 연속되어 있는 것.
- 등간 척도 ( 간격 척도 ) : 명목척도와 서열척도에 대한 정보를 가지면서도 등간 정보를 포함하는 것
ex, 온도 ( 0 도는 절대 0점이 아니다 )
- 비율 척도 : 앞의 모든 정보를 포함하면서 비율에 관한 정보를 담음.
절대 '0'의 값(절대영점)을 가지고 사칙연산 가능함 ex, 무게, 길이
02. 데이터의 표현 방법
001. 표
- 도수 분포표 : 도수분포표는 수집된 각각의 데이터에 대한 개수를 정리한 표
단점) 직관적으로 인식되는 형태가 아니어서 일일이 숫자로 비교해야함
002. 그래프
- 그래프 : 숫자를 일일이 살펴보지 않아도 크기나 형태 등을 바로 비교 가능

03. 기초 통계량
001. 중심경향도
: 중심경향도란, 데이터들을 종합하여 그 중심을 이루는 값이 어느 정도가 될지를 구한 것
1. 평균(mean)
: 평균(mean)은 통계에서 가장 많이 활용되는 중심경향도
-> 모든 통계분석에서 사용되며 표본의 특성을 제시할 때 가장 먼저 사용되는 수치

2. 중간값(median)
: 관측된 자료의 편중과 상관없이 가장 작은 값에서 가장 큰 값까지 정렬했을 때, 그 가운데 위치한 값
3. 최빈값(mode)
: 최빈값은 표본에서 가장 많이 나타나는 관측치
-> 여러번 확인된다는 특성으로 중심경향도에 있으나, 최소 부분과 최대 부분으로 쏠림 현상이 나타날 수도 있기 때문에, 특별히 필요성이 없는 한 잘 사용되지 않음
002. 산포도
- 표본의 특성이라 할 수 있는 분포의 정도를 나타내는 산포도를 확인해야 한다.
- 중심경향도만으로는 집단에 대한 성격과 분포를 파악하는데 부족하므로, 측정된 데이터가 어떻게 분포하고 있는지에 대해 파악해야 데이터를 제대로 이해할 수 있다.
1. 모분산(variance : var)
: 모평균과 모집단의 개별 측정치들 간의 차를 구해서 제곱하여 모두 더한 후, 그 값을 다시 모집단을 구성하는 개수로 나누어 계산
** 왜 제곱을 하는가 ? : ( 값 - 평균 )을 그냥 빼면, 오차의 + 와 - 가 되어 다 더하면, 0 이 되버림. 따라서 분산을 파악할 수 없음.
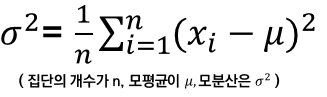

- 분산이 큼 : 값들이 퍼져있음. 평균이 값들의 특성을 잘 나타낸다고 말하기 어려움
- 분산이 작음 : 값들이 모여져있음. 값들이 평균값에 모아져 있음.
2. 표본분산( sample variance )
: 모집단을 기준으로 하지 않고, 표본을 선정해서 표본의 개수 (n-1)로 계산한 분산을 표본분산이라 한다.
** 자유도는 왜 n-1 이냐? : ex, A, B, C 의 값의 평균이 10이라면, A/B는 10 이상/이하이어도 상관 X, 하지만, A/B값이 정해져버리면, C의 값은 무조건 하나의 값으로 정해져야 평균이 10이 됨. 따라서, 자유롭게 값이 변할수 있는 것은 n-1개가 됨.

3. 표준편차( Standard Deviation )
: 분산과 편차의 개념은 평균으로부터 측정치들이 어느 정도 흩어져 있는지의 정도를 나타내는 것.
편차는 평균을 기준으로 음(-)과 양(+)으로 흩어져서 총합이 0이 되니, 이를 피하기 위해 편차에 제곱을 하는 것
-> 분산값에 루트를 씌워 제곱근을 만들면 표준편차가 됨.
4. 평균편차 ( Mean Deviation )
: 그룹에 대한 값 및 평균값 간 절대 차이의 평균으로 계산함.
** 하지만, 표준편차를 더 많이 사용하는 이유 : 평균 편차는 미적분을 해야하는데, 미분계수가 만들어 지지 않음.

공부 교재 : 제대로 시작하는 기초통계학
사회조사분석사
https://www.youtube.com/watch?v=jGOqkljySu8&list=PLsri7w6p16vuDN55ZGHVYnitXs2R1Wz6q
'DATA ANALYSIS > Math' 카테고리의 다른 글
| [Basic Statistics : CH 5. 추정] 점추정과 구간추정 , 모평균의 구간 추정, 모집단 비율 및 분산의 구간추정 (0) | 2020.12.01 |
|---|---|
| [Basic Statistics : CH 4. 확률분포] 확률분포, 이항분포, 포아송분포 (0) | 2020.11.10 |
| [Basic Statistics : CH 3. 확률과 통계] 확률과 의사결정, 확률변수의 기대값과 분산 (0) | 2020.11.08 |
| [Basic Statistics : CH 1. 모집단과 표본] 모집단과 표본 추출 , 표본의 분포 (0) | 2020.06.21 |
| [Python_Statistics : 1절 기초통계] 용어정리, 실험, 확률 변수와 확률 분포(이산형 확률변수) (0) | 2020.05.28 |




