| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- LSTM
- 자연어 논문
- airflow
- HackerRank
- 설명의무
- 표준편차
- Statistics
- 코딩테스트
- 자연어처리
- MySQL
- leetcode
- 자연어 논문 리뷰
- 서브쿼리
- NLP
- SQL 날짜 데이터
- update
- inner join
- 짝수
- sql
- 그룹바이
- sigmoid
- Window Function
- 논문리뷰
- torch
- SQL코테
- nlp논문
- CASE
- GRU
- 카이제곱분포
- t분포
- Today
- Total
HAZEL
[Python_Statistics : 1절 기초통계] 용어정리, 실험, 확률 변수와 확률 분포(이산형 확률변수) 본문
[Python_Statistics : 1절 기초통계] 용어정리, 실험, 확률 변수와 확률 분포(이산형 확률변수)
Rmsid01 2020. 5. 28. 15:291절. 기초 통계
1.1 용어 정리
- 모집단과 표본

1.2. 실험
- 실험 : 특정 목적 하에서 실험 대상에게 처리를 가한 후에 그 결과를 관측해 자료를 수집하는 방법
- 측정 : 추출된 원소들이나 실험 단위로부터 주어진 목적에 적합하도록 관측해 자료를 얻는 것.
- 표본 공간어떤 실험할 때 나타날 수 있는 모든 결과들의 집합
- 사건 : 표본공간에 있는 몇 개의 원소들로 이루어진 부분 집합
- 확률 : 특정 사건이 일어날 가능성의 척도 P(E) = n(E) / n(Ω)
- 확률변수 : 식
1.3. 확률 변수와 확률 분포
- 이산형 확률 변수 : 0 이 아닌 확률 값을 갖는 실수 값이 셀 수 있는 경우의 의미
ex , 이항 분포, 분포, 포아송 분포
- 연속형 확률 변수 : 가능한 값이 실수의 어느 특정 구간 전체에 해당하는 확률 변수를 의미함
ex, 균일 분포,정규분포, 지수분포지수 분포, t-분포, x **2 분포, F-분포 등
## 이산형 확률 변수 & Python
- 파이썬으로 이산형 확률 변수를 나타내기
0. 라이브러리
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline1. 이항 분포
: 어떤 시행에서 사건 X가 일어날 확률이 매회 p로 일정하다고 한다.
이 시행을 n회 독립적으로 반복할 때, 사건 X가 일어날 횟수를 확률변수 X라 하면 X의 확률분포
B(n, p)로 나타냄
* np.random.binomial(n, p [, size]) n번의 시도에 p 번의 가능성을 의미.
binomial_x = np.random.binomial(10, 0.5, 100)
binomial_x
- n = 10, p = 0.5 , size = 500
- n : 독립적 시행 횟수
- p : 각 시행이 가질 확률
- size : 개수(난수 발생) n을 몇 번 발생
- 0.5의 확률로 10번을 던지는데 , 그 행위를 100번 해라 라는 의미
plt.hist(binomial_x, bins=20 )
plt.show()
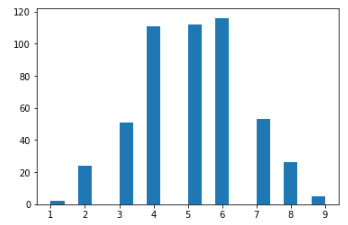
2. 베르누이 분포
: 결과가 두 개인 시행의 결과에 대하여 성공을 1 실패를 0으로 표시하는 확률변수.
이항 분포의 결과 중 하나라고 생각하면 됨.
* np.random.binomial(n=1, p [, size] )
- 이항 분포에서 n = 1 이면 베르누이 결과가 나옴.
bern_x = np.random.binomial(1, 0.5, 500)
plt.hist(binomial_x2, bins= 50 )
plt.show()

3. 기하 분포
: 베르누이 분포에서 처음 성공했을 때의 성공한 횟수 ex, 처음 앞면이 나오는 횟수.
* geometric(p [, size])
geom_x = np.random.geometric(p=0.5 , size = 500)
print(geom_x)
plt.hist(geom_x, bins =50),plt.show()
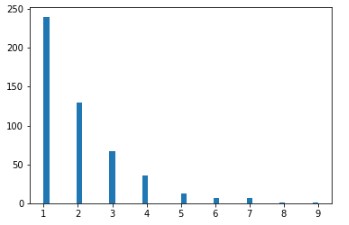
: 9번 안에는 무조건 앞면이 나왔다는 의미이다. 그런데, 랜덤이기 때문에, 그 이상의 수(ex, 12)도 나올 수 있다.
그때는 12번 만에 드디어 앞면이 나왔다는 의미가 된다.
* 위의 그래프를 축적된 합으로 나타낼 수 있다.
hist_ = plt.hist(geom_x, bins =10)
print(hist_)
plt.show()
hist_cumsum = np.cumsum(hist_[0])
print(hist_cumsum)
plt.bar(range(1,11), hist_cumsum)
plt.show()
4. 다항 분포
: 이항 분포를 확장한 것으로 세 가지 이상의 결과를 가지는 사건의 반복 시행에서 발생하는 확률분포이다.
k개 사건이 일어날 경우, (k-1) 차원의 이산형 분포를 갖는다.
* 이항 분포와 다항분포의 차이를 잘 확인해야 한다!
- 이항분포 : 주사위 1이나 오고 나머지가 나오냐!라는 의미
- 다항 분포 : 각각의 확률이 나오는 것
(통계에서는 pvals 쓸 때는 마지막 항은 안 적어도 되지만, 코드에서는 꼭! 적어줘야 한다.)
* multinomia(n, pvals [, size])
multinorm_x = np.random.multinomial(10, [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], 500)
multinorm_x
5. 포아송 분포
: 수리적으로 포아송 분포는 사건을 n회 시행할 때 특정한 사건이 y회 발생할 확률분포 중에서 사건을 시행한 수인 n이 무한대인 경우에 해당한다.
- lam : 정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기댓값, 그 이유는 이항 분포의 n* p = 평균이기 때문에.
람다 = 이항 분포의 n*p
ex, 상담원이 어떤 시간 안에 전화를 받는 기댓값
* poisson([lam, size]) : 람다 값이 필요
- size는 어떻게 분포가 형성될까를 알기 위해서!
pois_x = np.random.poisson(lam = 4, size = 100)
pois_x
plt.hist(pois_x, bins=50)
plt.show()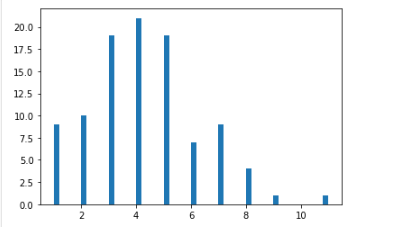
pois_x2 = np.random.poisson(lam = 10*1/6, size = 100)
pois_x2주사위를 10번 던졌을 경우 주사위 눈이 1이 나올 기댓값은 1.67 / 포아송이 분포를 따르는 난수 100개 생성
그 결과 데이터는 1.67 앞뒤로 더 많은 난수가 발생하는 것을 알 수 있음.


'DATA ANALYSIS > Math' 카테고리의 다른 글
| [Basic Statistics : CH 5. 추정] 점추정과 구간추정 , 모평균의 구간 추정, 모집단 비율 및 분산의 구간추정 (0) | 2020.12.01 |
|---|---|
| [Basic Statistics : CH 4. 확률분포] 확률분포, 이항분포, 포아송분포 (0) | 2020.11.10 |
| [Basic Statistics : CH 3. 확률과 통계] 확률과 의사결정, 확률변수의 기대값과 분산 (0) | 2020.11.08 |
| [Basic Statistics : CH 2. 데이터와 통계량] 데이터의 수집(척도), 데이터의 표현방법, 기초 통계량 (0) | 2020.11.06 |
| [Basic Statistics : CH 1. 모집단과 표본] 모집단과 표본 추출 , 표본의 분포 (0) | 2020.06.21 |




