| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 자연어 논문
- airflow
- sql
- 코딩테스트
- t분포
- 자연어처리
- MySQL
- GRU
- nlp논문
- 논문리뷰
- HackerRank
- LSTM
- 서브쿼리
- update
- Window Function
- leetcode
- NLP
- inner join
- Statistics
- 설명의무
- 표준편차
- 짝수
- 그룹바이
- CASE
- torch
- SQL 날짜 데이터
- 카이제곱분포
- 자연어 논문 리뷰
- SQL코테
- sigmoid
- Today
- Total
HAZEL
[Deep Learning 01 ] 얕은 신경망의 구조 ( Shallow Neural Network ) 본문
[Deep Learning 01 ] 얕은 신경망의 구조 ( Shallow Neural Network )
Rmsid01 2021. 1. 22. 16:11Deep Learning 01. 얕은 신경망의 구조
1. 인공 신경망 ( Artificial Neural Network )
1.1. 신경 세포(뉴런)
: 여러 신호를 받아, 하나의 신호를 만들어 전달하는 역할. 출력을 내기전에 활성 함수(activation function)을 통해 비선형 특성을 가할 수 있다. 앞 단계에서는 linear한 연산만 가능한데, 활성화 함수를 통해 비선형 특성을 가할 수 있게 된다.
: node는 단일 뉴런 연산 , edge는 뉴런의 연결성의 의미한다.
: 활성화 함수의 특징은 선형 함수가 아닌 비선형 함수여야 한다는 것이다.
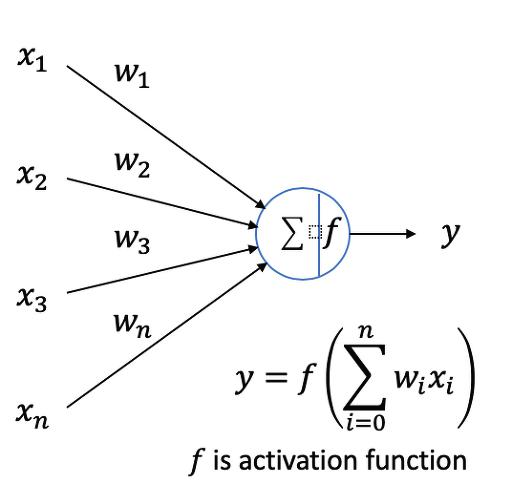
-> 입력이 들어오면, 각 입력에 가중치가 곱해지고 그것을 다 더한 후, 활성화 함수를 통과하는 과정을 거친다.
: 편향이 없다면, 뉴런이 표현할 수 있는 것이 원점을 지난 것으로 제한이 되기 때문에, 공식에 편향을 넣어준다.

: 뉴런은 수학적으로 두 벡터의 내적으로 표현할 수 있다.
1.2. 인공 신경망
: 뉴런이 모여 서로 연결된 형태를 인공신경망이라고 부름.
1.3. 전결합 계층 ( Fully - Connected Layer : FC Layer) = Dense Layer
: 이전 계층의 뉴런과 서로 모두 연결되어 있는 **계층( layer )
: 연결할 수 있는 가능성 모두 다 연결하는 것
** 계층 : 뉴런이 모인 한 단위


- 연결의 수는 입력과 출력 뉴런 갯수를 곱하면 나온다.

: FC 계층은 여러 개의 뉴런을 한 곳에 모아둔것으로, Matrix 곱셈 연산으로 표현됨.
- Tensorflow
# Tensorflow 2.X
# Dense Layer
tf.keras.layers.Dense(
units, activation=None, use_bias=True, kernel_initializer='glorot_uniform',
bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None,
activity_regularizer=None, kernel_constraint=None, bias_constraint=None,
**kwargs
)
- PyTorch
# PyTorch
# Linear
torch.nn.Linear(in_features, out_features, bias=True)
1.4. 얕은 신경망 ( Shallow Neural Network )
: input layer, hidden layer , output layer 3가지 계층으로 되어 있으며, 은닉 계층과 출력 계층이 Fully Connected 계층인 모델
: 얕은 신경망의 반대는 Deep Neural Network 이다.

1) 입력 계층 ( input layer )
: 입력을 받아서, 다음 계층으로 넘기는 역할만 하고, 연산을 일어나지 않는다.
: 무엇을 입력으로 주어야 하는가? -> 특징 추출 문제 (머신러닝에서는 특징추출을 직접 해줘야 함 )
: 계층의 크기 = Node의 개수 = 입력 스칼라의 수 = 입력 Vector의 길이.
: x = $ [x_0, x_1, x_2, ..., x_{n-1}]^T $
** 여기서는 행 벡터에 Transpose를 해주어, 열벡터를 의미하게 된다.
** x : 스칼라를 의미, x ( 이텔리체 ) : 벡터를 의미
2) 은닉 계층 ( Hidden Layer )
: 입력 계층과 연결된 전결합 계층으로, 얕은 신경망에서는 1개의 은닉 계층만 사용한다.
h = $ a_h(W_hx + b_h) $
3) 출력 계층 ( output layer )
: 은닉 계층 다음에 오는 전결합 계층으로 외부로 데이터를 전달한다.
: 신경망의 기능은 출력계층의 활성함수에 의해 결정된다. ( a )
: 출력 계층의 크기 = 출력의 스칼라 수 = 출력 vector 길이
y = $ a_o ( W_oh + b_o ) $
2. 인공 신경망을 이용한 회귀 모형
2.1. 회귀 ( Regresstion )
- 통계 파트에서 정리한 회귀분석 PART
2020/12/11 - [DATA/Math] - [Basic Statistics : CH 10. 회귀분석] 단순 회귀분석, 다중 회귀분석
[Basic Statistics : CH 10. 회귀분석] 단순 회귀분석, 다중 회귀분석
CH10. 회귀분석 01 . 단순 회귀분석 001. 단순회귀분석 ( Simple regression analysis ) : 원인과 결과 관계를 파악하는 것. : 하나의 변수가 다른 하나의 변수에 대해 미치는 영향을 파악하는 것 : 독립변수 X
hazel01.tistory.com
: 오차(잡음, noise )이 존재하는 train으로 부터 규칙을 찾아 연속된 값의 출력을 추정하는 것
: 학습 데이터를 통해서 회귀곡선(추세선)을 도출해내는 것.
1) 단순 선형 회귀 ( Linear Regression ) : 데이터를 가장 잘 표현하는 선형식을 찾는 동작
: 각각의 ( x , y ) 와 선형식의 차이 ( 오차 ) 가 최소화 되게 하는 것을 의미한다.
: 즉, 선형식 y= wx + b 에서 w와 b를 찾는 과정이 선형회귀를 의미.

2) 다중 선형 회귀
: 변수가 확장되어 벡터의 내적이 된다.
: 변수가 증가할 때마다, 차원이 하나씩 증가하게 된다. 직선 -> 평면 -> 초평면

2.2. 얕은 신경망을 이용한 회귀
: 얕은 신경망에서 회귀를 구하는 것은, hidden state에서 결정되는 것이 아니라, output layer의 활성화 함수에 의해 결정되게 된다. 회귀는 전 범위의 연속된 값을 output으로 하기 때문에, identity function ( 항등 함수 )를 사용한다.

: 얕은 신경망을 이용함에도 불구하고, 출력 계층의 공식은 선형회귀와 동일하다는 것을 확인 할 수 있다.
단지, 은닉 계층에서 데이터를 선형 회귀가 잘 되도록 변환이 있다는 점만 다르다!
( 조금 추상적인데,, 더 어떻게 설명해야 할지 모르겠다.. 나중에 헷갈리면 또 공부하자 ! )
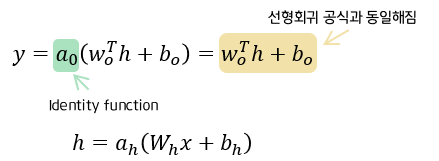
3. 인공 신경망을 이용한 분류 모형
3.1. 분류 ( Classification )
: 입력값을 특정 범주( Category ) 로 나누어주는 작업
: 나누어지게 그어주는 선을 - 분류곡선이라고 함. ( decision boundary )
- 카테고리가 2개이면, '이진 분류 ( Binary classification )' , 그 이상은 '다중 분류 ( Multi - class classification )
- 자연어처리 part 에서 정리한 텍스트 분류
2021/01/19 - [DATA/NLP] - [ NLP : CH8. 텍스트 분류 ] 나이브베이즈, 베이즈정리, RNN/ CNN으로 텍스트 분류(1D 합성곱),멀티 레이블 분류
[ NLP : CH8. 텍스트 분류 ] 나이브베이즈, 베이즈정리, RNN/ CNN으로 텍스트 분류(1D 합성곱),멀티 레이
8장. 텍스트 분류 ( text classification ) 8.1. 텍스트 분류? - 텍스트 분류란, 텍스트 / 문장 또는 문서를 입력으로 받아 사전에 정의된 클래스 중에서 어디에 속하는지 분류하는 과정 : 딥러닝 전, 나이
hazel01.tistory.com
3.2. 얕은 신경망을 이용한 분류
3.2.1. 이진 분류
: 분류 모형 역시, hidden state에서 결정되는 것이 아니라, output layer에서 결정되는데, 출력 계층을 보면 회귀 모형이랑 좀 다른 것을 볼 수 있다. 바로, 출력 노드가 하나라는 점이다. 또한, 활성 함수도 sigmoid 를 사용한다.
sigmoid는 이진 분류에서 사용되는 활성 함수이며, 0 ~ 1 사이의 실수 값을 출력값으로 가진다. 따라서, 0.5를 기준으로 첫 번째 class와 두 번째 class를 나눈다.

- Sigmoid 함수 특성 :
1. 값이 작아질 수록 0, 커질수록 1에 수렴하며, 출력이 0~1사이로 '확률'로 나타낼 수 있다.
그로인해, 이진분류에 적합한 함수가 된다.
2. 입력값이 0이 될 수록 출력이 빠르게 변하고, 무한대가 될수록 느리가 변한다.
3. 모든점에서 미분이 가능하며, 모든 실수 입력값에 대해 출력이 정의된다.
4. 0.5로 넘나 안넘나로 범주가 구분 됨.
def sigmoid(x):
return 1 / ( 1 + np.exp(-x))
1) 로지스틱 회귀 ( Logistric Regression ) : 범주형(카테고리) 데이터를 대상으로 하는 회귀, 분류기법
: 로지스틱 회귀는 데이터를 따라가는 식으로 회귀하는 선형회귀와 비슷하나, 범주형 데이를 분류하는 방향으로 선을 긋는다는 것이 차이점이다.
: 사람, 개 등으로 구분이 되는 것으로, 실질적으로 값의 의미를 가지는 것이 아닌 것을 범주형 데이터라고 함
( linear regression 은 실수형 )

- 교차 엔트로피 오차 ( Cross entropy error ; CEE ) : 정확히 맞추면 오차가 0, 틀릴수록 오차가 무한히 증가한다.

2) 다중 로지스틱 회귀
: 다중 로지스틱 회귀도, 다중 선형회귀 ( Linear Regression ) 처럼, 변수가 추가될수록 차원이 증가한다.
다만, 다중 선형회귀는 값을 따라서 예측하기 위해 선을 그어준다면, 로지스틱 회귀는 값을 구별하기 위해서 선을 그어준다.

: 로지스틱 회귀 역시, 얕은 신경망을 이용함에도 불구하고, 출력 계층의 공식은 로지스틱 회귀와 동일하다는 것을 확인 할 수 있다. 단지, 은닉 계층에서 데이터를 로지스틱 회귀가 잘 되도록 변환이 있다는 점만 다르다!
즉, 은닉계층에서는 shellow nn 을 이용해서, 선형적으로 분리가 잘 될 수 있도록 변형 시켜주는 것이다. 즉, decision boundary를 직선이 아닌 곡선으로 만들어주는 원리가 된다.

3.2.2. 다중 클래스 분류
: 다중 클래스 분류에서는 output 의 값이 해당 class에 속할 확률로 나온다. 즉, a일때의 확률, b일때의 확률, c일때의 확률이다. 이러한 결과값을 가지기 위해서 활성함수로 softmax를 사용한다.

: softmax 함수를 넣으면, a + b + c = 1 이 되며, 각각의 확률은 0보다 크거나 같고, 1보다 작거나 같다.
softmax 함수는 n개의 입력을 n개의 확률로 만들어준다.
- Softmax 함수 특성 :
1. 각 입력의 지수함수를 정규화 한것으로 각 출력은 0 ~ 1 사이를 가진다.
2. 모든 출력의 합은 반드시 1이 되며, 각각의 확률은 0보다 크거나 같고, 1보다 작거나 같다.
def softmax(x):
e_x = exp(x)
return e_x / np.sum(x)
- softmax 와 sigmoid의 비교
; 2 - class softmax 함수를 사용하는데, 하나의 값이 0으로 고정되어있다면, 그것은 sigmoid 의 정의와 같게 나오게 된다. sigmoid는 2가지 클래스를 구분하기위해 1개의 입력을 받는다.
$$ softmax([x,0])_0 = \frac{e^x}{e^x + e^0} = \frac{1}{1 + e^{-x}} $$
- multi class 일 경우, 교차 엔트로피 오차 : 정확히 맞추면 오차는 0, 틀릴수록 오차가 무한히 증가하는 특징을 가진다.





