| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Window Function
- LSTM
- update
- 서브쿼리
- 설명의무
- 자연어처리
- 논문리뷰
- inner join
- 그룹바이
- 자연어 논문
- torch
- MySQL
- 코딩테스트
- SQL코테
- 짝수
- sql
- 자연어 논문 리뷰
- 표준편차
- SQL 날짜 데이터
- CASE
- HackerRank
- t분포
- airflow
- GRU
- 카이제곱분포
- leetcode
- nlp논문
- Statistics
- NLP
- sigmoid
- Today
- Total
HAZEL
[ Deep Learning 02 ] 경사하강 학습법 ( Gradient Descent ) , 옵티 마이저 ( Optimizer ) 본문
[ Deep Learning 02 ] 경사하강 학습법 ( Gradient Descent ) , 옵티 마이저 ( Optimizer )
Rmsid01 2021. 1. 27. 00:35Deep Learning 02. 경사하강 학습법
1. 모델을 학습하기 위한 기본적인 용어
1.1. 학습 매개변수 ( Trainable Parameters )
: 학습 과정에서 값이 변화하는 매개변수
: 매개변수가 변화하면서, 알고리즘 출력이 변화됨.
: y = ax + b 일때, a 와 b를 의미함 , 즉, 가중치 W와 편향 b
1.2. 손실함수 ( Loss Function)
: 실제값과 예측값의 차이를 수치화 해주는 함수
: 실행하고 있는 학습 알고리즘이 얼마나 잘못하고 있는지를 나타내는 지표
: 지표의 값이 낮을수록 즉, 손실이 낮을 수록 학습이 잘 됬다는 것을 의미함.
: 정답과 알고리즘 출력을 비교하면서 손실을 구함.
-> 어떤 손실함수를 사용하냐에 따라서 학습이 어떻게 이루어지는지 결정됨
1.2.1. 손실함수의 종류
1. 평균 제곱 에러 ( Mean Squared Error ; MSE )
: 회귀 모델( 연속형 변수 예측 ) 에서 사용됨

2. 교차 엔트로피 오차 ( Cross entropy error ; CEE )
: 분류 모델에서 사용됨

# 이진 분류
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['acc'])
# 다중 클래스 분류
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['acc'])
1.3. 최적화 이론 ( Optimization Theory )
: '출력 값을 가장 작게 ( 또는 크게 ) 하는 입력값을 찾는 것
: loss function ( 손실함수 ) 를 최소로하는 입력 값을 찾아내는 것.
1.3.1. 최적화의 종류
1. 무차별 대입법 ( Brute - Force )
: 함수가 있을 때, 가능한 모든 수를 대입해서 output을 알아내는 것.
: 어떠한 알고리즘도 들어가지 않고, 정해진 범위에 대해 무차별적으로 대입하는 단순한 방법
- 특징
1) 최적값이 존재하는 범위를 알아야한다. 즉, 정해진 범위에 대한 사전정보를 가지고 있어야 한다.
2) 최적값을 정확히 알기 위해 무한히 촘촘하게 조사를 해야한다.
3) 따라서, 최적값을 알기위한 계산 복잡도가 매우 높아진다.
-> 이러한 이유로, 최적화를 위해서 잘 사용되지 않는다.
2. 경사하강법 ( Gradient Descent )
: 경사를 따라 여러번의 스텝을 통해 최적점으로 다가가는 것.
: 경사는 기울기 ( 미분, Gradient )를 이용해서 계산을 진행한다.
1.3.2. 최적화 방법
1. 분석적 ( Analytical method )
: 함수의 모든 구간을 수식적으로 알때, 사용하는 수식적인 해석 방법
: 위에서 언급한, 무차별 대입법과 같은 맥락이다.
- 정해진 범위 즉, 수식을 알아야 사용이 가능하다.
2. 수치적 방법 ( Numerical method )
: 함수의 형태와 수식을 알지 못할 때, 사용하는 계산적인 해석 방법으로, 대표적인 방법이 '경사하강법' 이다.
: 딥러닝을 이용하면, model의 수식이 어떤 상황인지 알수 없는 상황이 된다.
=> 최적화 : 딥러닝에서 손실함수가 최소가 되게하는 파라미터를 구하는 것
2. 경사하강법 ( Gradient Descent )
2.1. 경사하강법
: 경사를 따라 여러번의 스텝을 통해 최적점으로 다가가는 것.
: 경사는 기울기 ( 미분, Gradient )를 이용해서 계산을 진행한다.
: 시작점은 랜덤하게 정해준 후, 경사하강법에 따라서, 최적값을 찾는 것.
2.1.1. 미분 ( 1차원에서의 미분 )
: x가 변할 때, y가 변하는 값을 의미한다.
$$ \frac{df(x)}{dx} = \lim_{\Delta x \rightarrow 0}\frac{f(x+\Delta x) - f(x)}{\Delta x} $$
2.1.2. 기울기 ( n차원의 gradient )
: 여러 축을 가지는 x 를 각 방향으로 편미분하여, 벡터로 늘여둔 것이 gradient 다.
: 즉, 각 축에 대해 미분을 각 각 한것이다.
: ex, 3차원일 경우 $ x_0, x_1, x_2 $ 에 대해 3가지 방향으로 각각 편미분을 한다.
: x는 여러축을 가지는데, 즉, n개의 축 ( n개의 입력 ) 을 가지나, 미분하여 1개의 출력값을 가진다.
: 스칼라를 벡터로 미분한 것
$$ \bigtriangledown f(x) = \begin{bmatrix}
\frac{df(x_0)}{dx_0}, & \frac{df(x_1)}{dx_1} ,& ... ,& \frac{df(x_{N-1})}{dx_{N-1}}
\end{bmatrix}^T $$
2.1.3. 경사하강법의 한 스텝
1) 1 - D의 경우
$$ x_n = x_{n-1} - \alpha \frac{dfx_{n-1})}{dx} $$
: gradient 에 α ( 학습률 ) 을 곱한다.
: - 를 붙인 이유는 스텝이 전역 최솟값의 좌측에서 시작한 경우 기울기는 음(-)의 값을 가지므로, -와 만나 +가 되어 θ값을 키워 우측으로 이동해야 하기 떄문이다.
2) N - D의 경우
$$ x_n = x_{n-1} - \alpha \bigtriangledown f(x_{n-1}) $$
: x 벡터인 $ x_n , x_{n-1} , \bigtriangledown f(x_{n-1}) $ 은 N X 1 값을 가짐
=> 경사하강법은 변수의 스케일에 따라서도 문제가 발생한다. 변수 a의 스케일이 작으면, 세타의 크기를 크게 바꿔야 하는데, 그러면 훈련 시간이 오래 걸리게 된다. 따라서, 모든 변수들이 같은 스케일을 갖도록 스케일링을 해줘야 한다.
< 사이킷런에선 standardScaler 을 통해 표준화 할수 있다 >
2.2. 학습률 ( Learning rate )
: 경사하강법이 이동하는데, 이 학습률 α에 비례(α를 곱해서) 하여 이동한다. 따라서, 적절한 학습률을 선택해야, 최적의 값을 구할 수 있다.
: 하강하는 폭 ( step ) 을 의미한다.
- α : 상수값 / 하이퍼 파라미터

2.2.1. 학습률이 너무 작은 경우
: 학습속도가 느려지는 결과가 발생
: 굴곡이 있는 비용함수 ( 변곡점이 많은 ) 경우 전역 솔루션을 찾지 못하는 경우도 있다.
2.2.2. 학습률이 너무 큰 경우
: 한 스텝의 크기는 기울기의 크기에 비례하므로, 최적값에 잘 도달하지 못하고, 진동하는 특성을 보인다.
- 기울기 폭주(Gradient Exploding)
: 기울기가 점차 커지더니 가중치들이 비정상적으로 큰 값이 되면서 결국 발산되는 것
: 학습률이 극단적으로 크면 값이 발산 하여, f(x)값이 무한대(inf) 로 가게 된다.
: 즉, x값이 정의되지 않게 된다. ( x는 nan 이 됨. )
=> 따라서 적절한 학습률을 선택하는 것이 중요하다.
2.3. 볼록함수 vs 비 볼록 함수
2.3.1. 볼록 함수 ( Convex Function )
: 어디서 시작하더라도 경사 하강법으로 최적 값에 도달할 수 있다.
2.3.2. 비 볼록 함수 ( Non - Convex Function )
: 시작 위치에 따라 다른 최적값을 찾는다. 즉, 지역 최적값( local minimum)에 빠질 위험이 있다.

** 전역 솔루션 ( Global solution ) : 정의역 ( Domain ; x값이 존재하는 집합 ) 에서 단 한개 존재한다.
** 지역 솔루션 ( Local solution ) : 주어진 함수내에 여러개일 수 있으며, 시작 위치에 따라 다르다.
2.4. 기본적인 경사하강법에 대한 한계점
1. 대부분의 모델은 비볼록 함수이므로, 단순한 경사 하강법으로는 초기값에 따라 local minimum에 빠질 위험이 있다.
2. 경사 하강법은 안정점 ( saddle point )에서 벗어나지 못한다.
** 안정점 : 기울기가 0이 되지만, 극값이 아닌 지점
2.5. 경사하강법 방법 [ 옵티 마이저 ; Optimizer ]
2.5.1. 배치 경사 하강법 ( Batch Gradient Descent )
: 기본적인 경사하강법으로, 옵티마이저 중 하나로 오차를 구할 때 전체(일괄) 데이터를 고려함.
: 머신러닝에서 전체 데이터를 1번 훈련 = 1 에포크라고 하는데, 배치 경사 하강법은 한 번의 에포크에 모든 매개 변수 업데이트를 단 한번 수행한다.
: 전체 데이터를 고려해서 학습하므로, 에포크당 시간이 오래 걸리며, 메모리를 크게 요구한다.
: 하지만, 글로벌 미니멈을 찾을 수 있다
$$ x_n = x_{n-1} - \alpha \bigtriangledown f(x_{n-1}) $$
model.fit(X_train, y_train, batch_size=len(train_X))
2.5.2. 확률적 경사 하강법 ( SGD , Stochastic Gradient Descent )
: 매개변수 값을 조정시 ( 매 스텝 ( step ) 에서 ), 전체 데이터가 아니라 랜덤으로 선택한 딱 1개의 샘플에 대해서 gradient를 계산한다.
- 랜덤으로 1개의 샘플을 선택하므로, 한 epoch에서 여러번 선택될 수 있고, 안 쓰일 수도 있다.
< 한 epoch 마다 다른 샘플을 사용하려면 차례대로 하나씩 선택하고 다시 섞는 방식을 사용할 수 있다. SGDRegressor / SGDClassifier>

- 장점
1 ) 더 적은 데이터를 사용하므로 더 빠른 계산을 할 수 있다. 속도는 배치 경사하강법보다 빠르다.
2 ) 매 반복에서 적은 데이터를 처리하고, 1개 샘플에 대한 메모리만 필요함로 매우 큰 훈련 데이터 셋도 가능하다.
3 ) 매개 변수의 변동폭이 요동치는 것으로 지역 최솟값을 뛰어넘어 전역 최솟값을 찾게 도와줄 수 있다.
- 단점
1) 확률적이기 때문에 매개변수의 변동폭이 불안정해서, 배치 경사 하강법보다 정확도가 낮을 수도 있다.
=> learning rate을 크게 설정하고 점차 작게 줄여서 전역 최솟값에 도달하게 하는 것이 좋다. 이러한 과정을 학습 스케쥴 ( learning schedule ) 이라고 한다.
model.fit(X_train, y_train, batch_size=1)
2.5.3. 미니 배치 경사 하강법 ( Mini - Batch Gradient Descent )
: 전체 데이터도 아니고, 1개의 데이터도 아니고 정해진 양에 대해서만 계산하여 매개 변수의 값을 조정하는 경사하강법
: 전체 데이터를 계산하는 것보다 빠르며, SGD보다 안정적인 장점이 있다.
-> 경사하강법 방식에 비해 정확도가 떨어 진다는 얘기가 있지만, 연구결과 차이가 미비하고 오히려 더 좋은 성능을 낸 경우가 있다.
: 하지만, 지역 최솟값에 빠져나오기는 조금 더 힘들 수 있다.
model.fit(X_train, y_train, batch_size=32) #32를 배치 크기로 하였을 경우
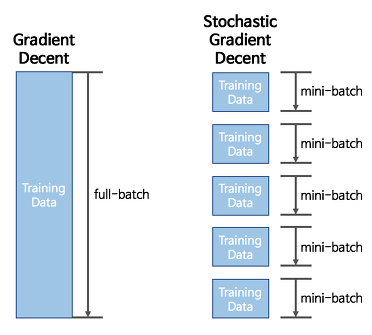
요즘은 관용적으로 mini batch stochastic gradient descent를 stochastic gradient descent( 확률적 경사하강법, SGD ) 라고 말한다고 한다.
※ 옵티마이저의 발전 과정


- 옵티마이저의 발전과정은 gradient 와 learning rate 를 어떻게 수정했냐에 따라서 달라진다.
- Gradient 수정 : Momentum , Nag
- Learning Rate 수정 : Adagrad, RMSProp, AdaDelta
- 두가지를 합한 것 : Adam , Nadam
2.5.4. 모멘텀 ( Momentum )
: 관성이라는 물리학 법칙 처럼, 이동 벡터를 이용해 이전 기울기의 영향을 받도록 하는 것.
: 이전 벡터의 이동의 크기를 현재에 반영해주는 것이다.
- 즉, 로컬 미니멈에 도달하여 기울기가 0이여도, 이전의 기울기를 가져와서 움직이기 때문에 로컬 미니멈을 탈출하는 효과를 얻을 수 있다. 하지만, 이동 벡터를 추가하면서 그 값을 기억해야 하기 때문에, 경사 하강법 대비 2배의 메모리를 사용하게 된다.

수식은 너무 싫지만,, 수식을 보면 조금 더 직관적일 때가 있다. 위의 수식을 보면 기존의 경사하강법에서 γ 와 ( t-1 ) step의 x 이동 벡터를 곱해준 값으로 t번째 step에서의 x의 이동 벡터를 구하는 것을 볼 수 있다.
즉, $ γ v_{t-1} $ 부분이 '기존 경사 하강법'과의 차이다.
아래 코드를 보면, momentum = 0.9 로 되어있는데, 관성 계수는 하이퍼파라미터 이며 0.9로 설정해준다.
keras.optimizers.SGD(lr = 0.01, momentum= 0.9)
2.5.5. 아다그라드 ( 적응적 기울기 , Adaptive gradient ; AdaGrad , 에이다그라드 )
: 변수별로 학습율이 달라지게 조절하는 알고리즘
: 매개변수들은 각자 의미하는 바가 다른데, 모든 매개변수에 동일한 학습률을 적용하면 비효율적이게 됨. 따라서, adagrad는 각 매개변수에 서로 다른 학습률을 적용 시킨다.
: 이때, 기울기가 커서 변화가 많은 매개변수는 학습률을 감소시켜, 다른 변수들이 잘 학습되도록 한다.

- $ (\bigtriangledown f(x_{n-1}) )^2 $ : gradient 의 스칼라를 제곱
- $ g_t $
: t 번째 step까지의 기울기의 누적 크기
: gradient 크기를 누적해서 더해 주는 것을 의미함. 즉, gradient에 비례해서 이동하게 해줌
-> 현재까지 얼만큼 gradien에 대해서 이동을 했는지 각 변수에 따라서 각각 계산을 해주는 역할
- $ x_t $ 를 구할 때, $ \sqrt{g_t + \epsilon } $ 을 나누는 것
: 위에서 구한 누적 크기를 나누어 줌으로써 , 학습이 많이 된 것을 나눠서 줄여주는 효과를 가짐. 제곱근을 한 것은 위에서 제곱을 해줬기 때문이다.
- ϵ
: $ g_t $ 가 0 에 가까우면 무한대로 튀는 문제가 발생하기 때문에, ϵ 를 더해줘서 분모가 0 이 되지 않게 해줌
keras.optimizers.Adagrad(lr=0.01, epsilon=1e-6)
- 하지만, $ g_t $ 가 누적하여 커지며, 한번 커진 값은 줄어들지 않기 때문에 오래 진행되면 더이상 학습이 이루어지지 않는 단점이 있다. 이러한 단점을 개선하기 위해서 , RMSProp 가 등장하였다.
2.5.6. RMSProp
: AdaGrad의 문제점을 개선한 것으로, 합 대신 지수 평균을 이용하였다.
: 변수 간의 상대적인 학습차이를 유지하면서, $ g_t $ 가 무한정 커지는 것을 막아 학습을 오래 할 수 있다.
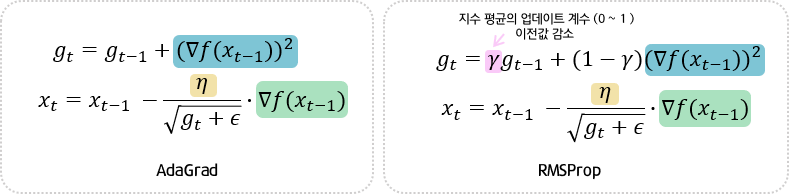
- 아래 코드에서의 하이퍼파라미터는 위의 수식과 연관 되어있다.
- learning rate , 지수 평균의 업데이트 계수, 엡실론 을 지정해준다.
keras.optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=1e-06)
2.5.7. Adam ( Adaptive moment estimation ; 아담 )
: RMSProp 와 Momentum의 장점을 결합한 알고리즘. 가장 최신의 기술이며 딥러닝에서 가장 많이 사용됨.

keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False)
** 본 게시글은 아래 출처를 참고하여 공부하면서 작성하였습니다.
'DATA ANALYSIS > ML & DL' 카테고리의 다른 글
| [ PyTorch 02. ] Data Preprocess , DataLoader, 데이터 시각화 (0) | 2021.04.30 |
|---|---|
| [ PyTorch 01. ] Basic, Operations, View, Slice and Index, Compile, AutoGrad (0) | 2021.04.29 |
| [Deep Learning 01 ] 얕은 신경망의 구조 ( Shallow Neural Network ) (0) | 2021.01.22 |
| [Deep Learning 03 ] GRU ( Gated Recurrent Unit ) (0) | 2020.12.26 |
| [Deep Learning 02 ] LSTM ( Long Short - Term Memory ) (0) | 2020.12.21 |




