| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- NLP
- leetcode
- t분포
- sql
- Statistics
- 코딩테스트
- nlp논문
- torch
- SQL코테
- update
- 자연어 논문
- HackerRank
- 카이제곱분포
- MySQL
- 그룹바이
- 논문리뷰
- 설명의무
- 자연어 논문 리뷰
- sigmoid
- 서브쿼리
- 자연어처리
- airflow
- 짝수
- CASE
- 표준편차
- GRU
- Window Function
- inner join
- LSTM
- SQL 날짜 데이터
- Today
- Total
HAZEL
[ NLP : CH8. 텍스트 분류 ] 나이브베이즈, 베이즈정리, RNN/ CNN으로 텍스트 분류(1D 합성곱),멀티 레이블 분류 본문
[ NLP : CH8. 텍스트 분류 ] 나이브베이즈, 베이즈정리, RNN/ CNN으로 텍스트 분류(1D 합성곱),멀티 레이블 분류
Rmsid01 2021. 1. 19. 16:088장. 텍스트 분류 ( text classification )
8.1. 텍스트 분류?
- 텍스트 분류란, 텍스트 / 문장 또는 문서를 입력으로 받아 사전에 정의된 클래스 중에서 어디에 속하는지 분류하는 과정

: 딥러닝 전, 나이브 베이지 분류 ( Naive Bayes classification ), SVM(support-vector machine) 등 존재함
8.2. 나이브 베이즈
: 나이브 베이즈는 간단하지만, 매우 강력한 분류 방식. 단어를 불연속적인 심볼로 다루는 만큼 아쉬운 부분도 존재함
나이브 베이즈를 이해하기 위해서는, 베이즈 정리를 이해해야 하기 때문에, 아래에 먼저 베이즈 정리를 다루겠음.
8.2.1. Bayesian Theorem ( 베이즈 정리 )
: 데이터 D가 주어졌을때, 각 클래스 c의 확률 = P(c|D)
: 베이즈 정리에서의 확률이란, 빈도주의 관점이 아닌, 베이지안 주의 관점인데, 즉! '주장에 대한 신뢰도' 를 의미한다.
- 확률론 패러다임의 변화 : 연역적 추론에서 귀납적 추론
: 기존의 통계학은 '빈도주의' 관점을 기반으로 구성되어있으며, 연역적 추론으로 구성되어있다. 그러나, 베이지안 관점에서는 불확실성을 내포하는 수치를 기반으로 하고, 그 수치를 바탕으로 사전확률을 갱신한다.
- 명칭
1. P(c) : Prioi
: A의 사전확률. 어떠한 사건에 대한 정보가 없을 때의 확률
: 어떤 사건이 발생했다는 주장에 관한 신뢰도
2. P(c|D) : Posteriori
: B에 대한 A의 사후확률. B라는 정보가 주어졌을 때 확률
: 새로운 정보를 받은 후 갱신된 신뢰도를 의미
3. P(D) : evidence - 새로운 정보
4. P(D|c) : likelihood
- 베이지안 정리 수식

: 대부분의 문제에서는 P(D)를 구하는 것이 어려우므로, P(c|D) ∝ P(D|c)P(c) 로 접근 함 ( ∝ : 비례관계 )
-> 사후 확률을 최대화하는 클래스 c를 구하는 것을 '사후 확률 최대화 ( Maximum a posterior : MAP ) 라고 함.

8.2.2. MAP : 사후 확률 최대화 ( Maximum a posterior )
: D(데이터)가 주어졌을 때, 가능한 클래스의 집합 c중 사후확률을 최대로하는 클래스 D를 선택하는 것
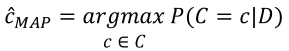
8.2.3. MLE : 최대 가능도 추정 ( Maximum Likelihood Estimation )
: 데이터 D가 나타날 가능도를 최대로하는 클래스 D를 선택하는 것
: 모수적인 데이터 밀도 추정방법으로서, 파라미터 θ = ( θ1, ... θm ) 으로 구성된 어떤 확률밀도함수 P(x|θ)에서 관측된 표본 데이터 집합을 x = (x1, x2,..., xn)이라 할때, 이 표본들에서 파라미터 θ를 추정하는 방법

MLE는 주어진 데이터 D와 클래스 레이블 c가 있을때, 확률 분포를 근사하기 위한 함수 파라미터 θ를 훈련하는 방법으로 쓰임
[ hazel01.tistory.com/manage/newpost/23?type=post&returnURL=https%3A%2F%2Fhazel01.tistory.com%2F23 ]
-> MAP는 경우에 따라서 MLE에 비해 더 정확할 수 있는데, 그 이유는 '사전 확률이 반영되어있기 때문'이다.
8.2.4. 나이브 베이즈
: 나이브 베이즈는 MAP를 기반으로 동작함. 베이즈 정리를 이용해 만든 확률 분류기의 일종
: 각 클래스에 대한 가능도 비교를 통한 분류
대부분의 경우, 사후 확률을 바로 구하기가 어렵기 때문에, 가능도와 사전확률의 곱을 통해 클래스 y를 예측함.
- prior(기존 정보)에, 추가 정보 즉, likelihood 를 곱해주어 판단 근거를 찾을 수 있다.
=> 판단근거 = 사전지식(prior) x 추가정보(likelihood) 가 되는 것이다.
이때, 추가 정보가 1개가 아니라 여러개라면, naive (순진하게) 그냥 다 곱해준다.

이런 방식으로 판단 근거를 도출해 낼 수있다.
따라서, 우리가 구하고자 하는 MAP를 활용한 클래스는 이러한 사후확률을 최대화하는 클래스이다.
즉, 나이브 베이즈 가정에 따라 각 특징들의 확률의 곱에 사전확률을 곱한 값을 최대화 하는 클래스와 같다.
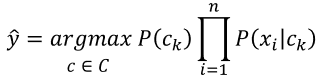
** 자연어처리에서 나이브 베이즈
- 보통 확률은 코퍼스의 출현 빈도를 통해 추정 -> 특징이 복잡할 수록 가능도 또는 사후확률을 만족하는 코퍼스는 드물다. 이런 경우, 각 특징이 독립적이라고 가정하는 나이브 베이즈를 이용하여, 각 특징의 결합 확률을 각 독립된 확률의 곱으로 근사할 수 있다.
- 사전확률
: 사용되는 사전 확률은 아래와 같이 실제 데이터(코퍼스)에서 출현한 빈도를 통해 추정할 수 있다.

- 특징별 가능도 확률
: 모든 특징의 조합이 데이터에 실제로 나타난 횟수를 통해 확률을 구하려고 하면, 희소성 문제 생김. 하지만, 나이브 베이즈의 가정을 통해 데이터 또는 코퍼스에서 출현 빈도를 구할 수 있다.

8.2.5. 예제 : 감성 분석
: 텍스트 분류 기법에서 많이 사용되는 감성 분석은 사용자의 댓글이나 리뷰 등을 긍 부정으로 분류하는 방법이다.
C = { 긍, 부 } , D = { d1, d2 ,... } : 문서로 구성
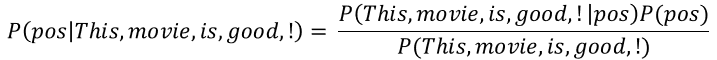
: 나이브 베이즈를 이용하여, 단어의 조합에 대한 확률을 각각 분해할 수 있다.

: 확률을 데이터 D에서의 출현 빈도를 통해서 구할 수 있다.
8.2.6. add- one Smoothing ( 라플라스 스무딩 (Laplace Smoothing).)
- 나이브 베이즈 가정의 문제 : 훈련 데이터에서 Count(good, neg) = 0이라면, P(good , neg ) = 0이 된다. 존재하지 않는다는 이유로, 0이 되는 것은 위험한 일이 된다. 이때, 각 출현 횟수에 1을 더해주면 이러한 문제를 해결할 수 있다. 완벽하진 않아도, 간단하면서 좋은 성능을 보인다고 한다.

8.2.7. 장점과 한계
- 장점 : 단순히 출현 빈도를 세는 것처럼 쉽고 간단하게 구현할 수 있다. 레이블당 문장 수가 매우 적으면, 복잡한 딥러닝보다 더 나은 성능을 보일 수 있다.
- 단점 : 문장의 출현 여부만 적용하기 때문에, 순서로 인해 생기는 관계와 정보를 무시한다. 왜냐하면, 나이브 베이즈는 '각 특징이 서로 독립적이다'라는 특징을 가지고 있기 때문이다. 즉, I don't like는 좋아하지 않다지만, don't와 like를 따로 반영하기 때문에, 문장을 정확하게 분류하는데 한계를 가지고 있다.
8.3. 반드시, 표제어 추출 혹은 어간 추출을 수행해야 할까?
- 표제어 추출 혹은 어간 추출처럼 문장을 전 처리하여, 코퍼스로 나타나면, 결과를 얻을 때, 희소성 문제를 어느 정도 해결할 수 있다. 하지만, 딥러닝을 이용하기 시작하면서 '차원 축소'라는 방법이 생겨 이러한 전처리가 반드시 정석이라고 말할 수 없다. 따라서, 이 [ 김기현의 자연어 처리 딥러닝 캠프 ] 저자는 , 먼저 표제어 및 어간 추출을 하지 않은 상태에서 딥러닝 모델을 사용하여 베이스 모델을 만드는 것을 추천했다. 이후, 튜닝 및 시도를 할 때 하나의 방법으로 표제어 및 어간 추출을 하는 것을 말했다.
8.4. 딥러닝을 활용하여 텍스트 분류하기
: 텍스트 분류하는 다양한 방법이 있겠지만, 이 책에서는 RNN과 CNN을 언급했다.
8.4.1. RNN으로 분류하기
: RNN에 대한 자세한 내용은
2021/01/19 - [DATA/NLP] - [ NLP : CH7. 시퀀스 모델링 ] 순환 신경망, LSTM, GRU, 그래디언트 클리핑
model.add(SimpleRNN(hidden_size, input_shape=(timesteps, input_dim)))- SimpleRNN 대신, GRU LSTM 을 넣어서 사용해도 됨.
- hidden_size = 출력의 크기 ( output_dim ) , timesteps = 시점의 수 ( 각 문서에서의 단어 수 )
- input_dim = 입력의 크기 ( 각 단어의 벡터 표현의 차원 수 )

- 감성 분석은 Many to one ( 다 대 일) 문제에 속하기 떄문에, 모든 시점에 대해 입력을 받지만, 최종 지점의 RNN셀만이 은닉 상태를 출력하게 된다. 이 것이 출력층으로 가서, 활성화함수를 통해 분류를 하게된다.

8.4.2. CNN으로 분류하기
: 합성곱 신경망(CNN)계층을 활용한 텍스트 분석 - 1D 합성곱 ( 1D Convolutions )
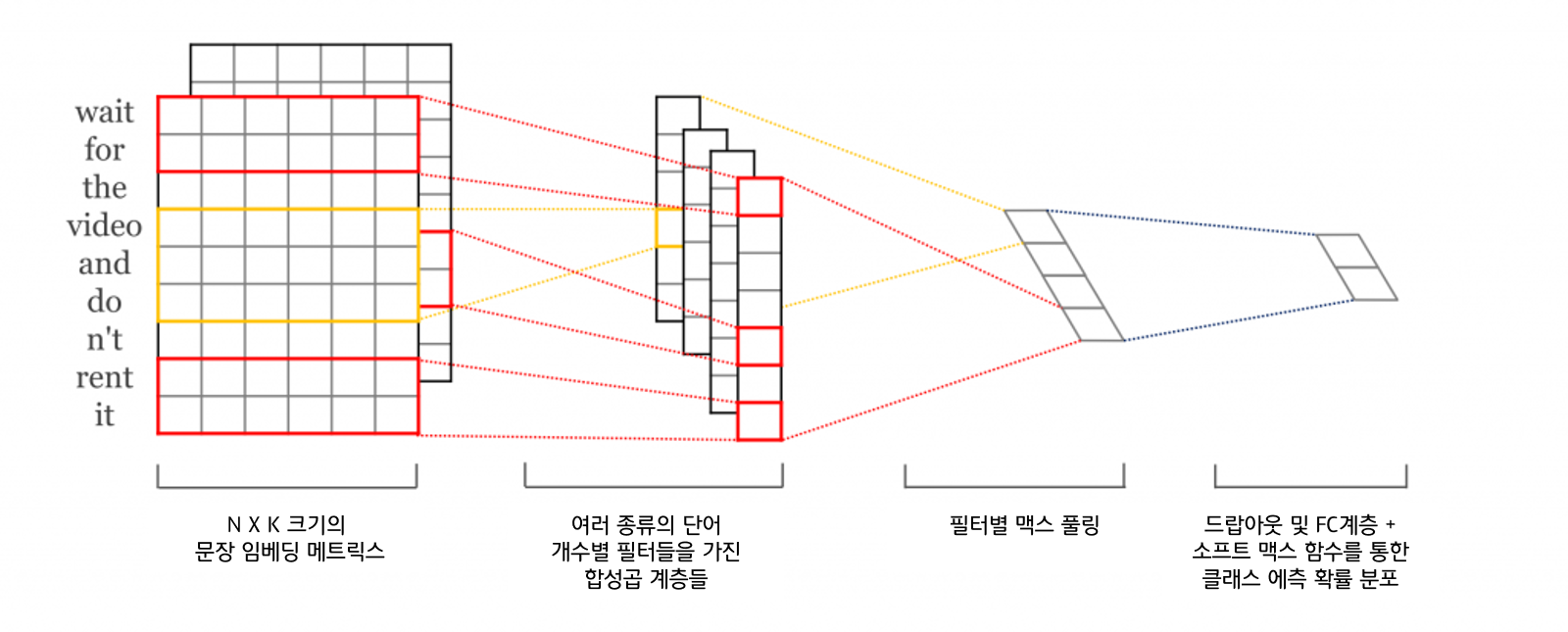
1) N X K크기의 문장 임베딩 메트릭스 : 문장을 토큰화, 패딩, 임베딩층을 거쳐서, 임베딩 매트릭스를 만든다.
2) 여러 종류의 단어 개수별 필터들을 가진 합성곱 계층들
- 1D CNN은 너비방향으로 움직일 수 없기때문에, 커널이 문장 행렬의 높이 방향으로만 움직임. 위의 사진에서의 빨간색은 커널 K =2 이며, 노란색 커널사이즈 = 3이다.
- 2D CNN의 커널 사이즈를 조절할 수 있는 것처럼, 1D CNN에서도 커널 사이즈를 조절할 수 있다. 그러나, 넓이는 임베딩 사이즈로 고정됨을 볼 수 있다.
- 커널은, 신경망 관점에서 가중치 행렬이므로, 커널의 사이즈에 따라 학습되는 파라미터의 수가 달라짐. 즉, NLP에선 커널의 사이즈에 따라 참고하는 단어의 묶음 크기가 달라짐을 의미한다. 즉, 참고하는 N-gram이 달라진다고 볼 수 있다.

3) 필터별 맥스 풀링 (max-pooling)
- 맥스 풀링 : 각 합성곱 연산으로부터 얻은 결과 벡터에서 가장 큰 값을 가진 스칼라 값을 빼는 것.

4) 드랍아웃 및 FC계층 + 소프트 맥스 함수를 통한 클래스 예측 확률 분포
: 이진분류이지만, 시그모이드 함수가 아니라 소프트맥스 함수를 사용하므로 출력층에서 뉴런의 개수가 2인 신경망을 설계함
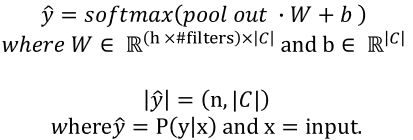
5) 전체 신경망 아키텍쳐
이미지 출처 : 논문 A Sensitivity Analysis of (and Practitioners' Guide to) Convolutional Neural Networks for Sentence Classification
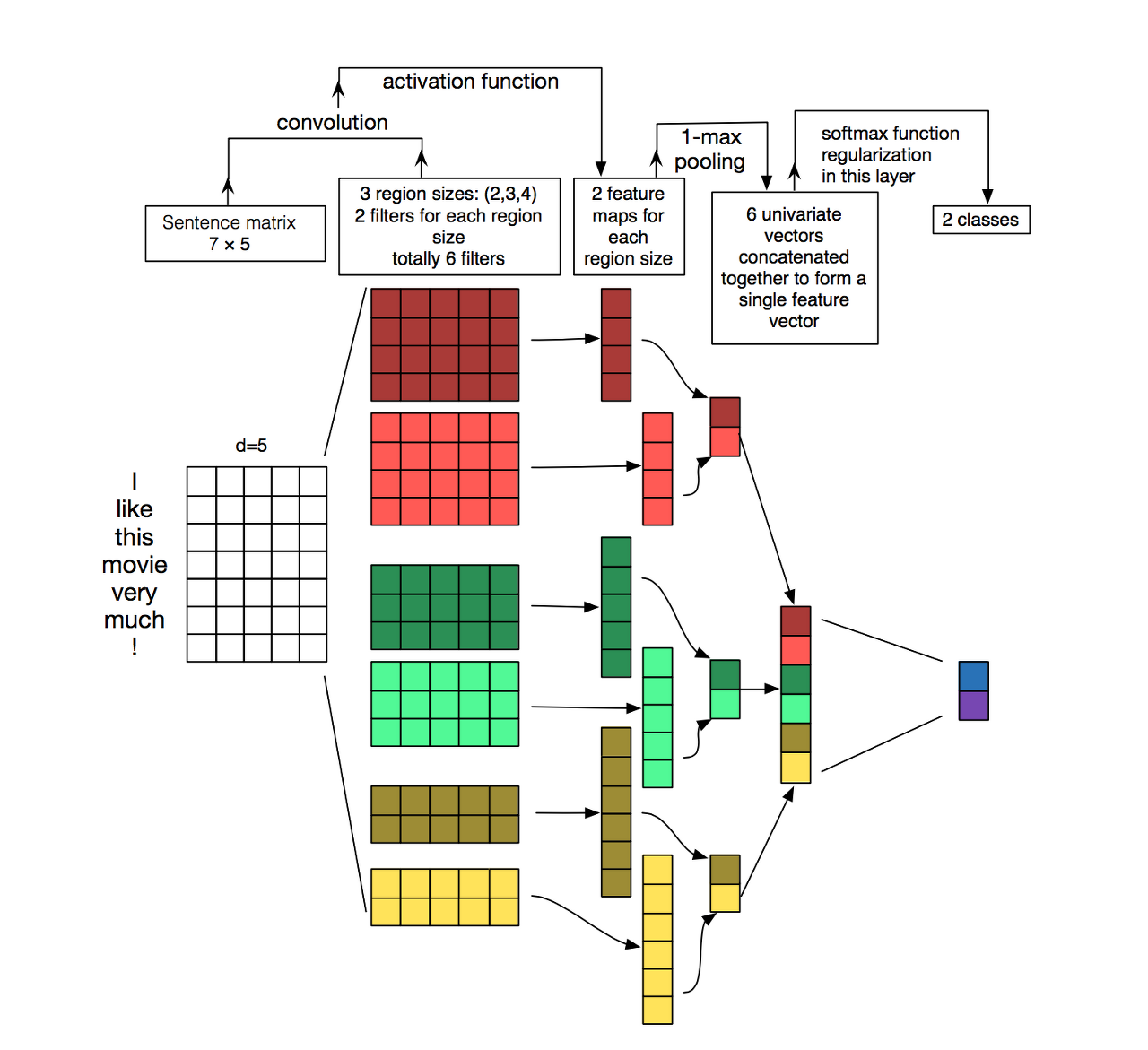
: 여기에 RNN을 활용한 텍스트 분류 처럼, 교차 엔트로피 손실함수를 적용하여 이를 최소화 하도록 최적화를 수행하면 CNN 신경망도 훈련이 됨.
8.5. 멀티 레이블 분류 ( Multi-label Classification )
: 기존의 소프트맥스 분류와는 달리 여러 개의 클래스가 동시에 정답이 될수 있는 것을 의미함.
: 기존의 소프트맥스 분류는 문장의 클래스가 여러 후보중에 한 개만 해당됨.
예 ) 의상 데이터가 존재하는 경우, 옷의 종류와 색을 동시에 분류하는 것
** 멀티 클래스 분류 : 의상 데이터가 존재하는 경우 , 빨간 옷 / 파란옷 / 초록 옷 으로 분류하는 것
8.5.1. 이진 분류 ( binary classification )
: 마지막 계층은 1개의 노드에 시그모이드 함수를 사용하는 것.

: 이진 분류에서는 아래의 수식을 항상 만족한다.

: 이진 분류에서는 sigmoid함수를 사용하며, 손실함수로는 Binary cross entropy loss (BCEloss) 함수를 활용한다.
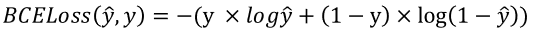
: 이 수식에서 y 는 0또는 1의 값을 가지는 불연속적인 값이다. y ̂는 시그모이드함수의 출력값이 된다.
8.5.2. 멀티 이진 분류
' 이진 분류를 이용하여 멀티 레이블 분류를 적용하기 '
: 분류 문제에 대해서 신경망 마지막 계층에 n개의 노드를 주고 모두 시그모이드 함수를 적용하면 된다.
-> 하나의 모델로 여러개의 이진 분류 작업을 수행할 수 있다.
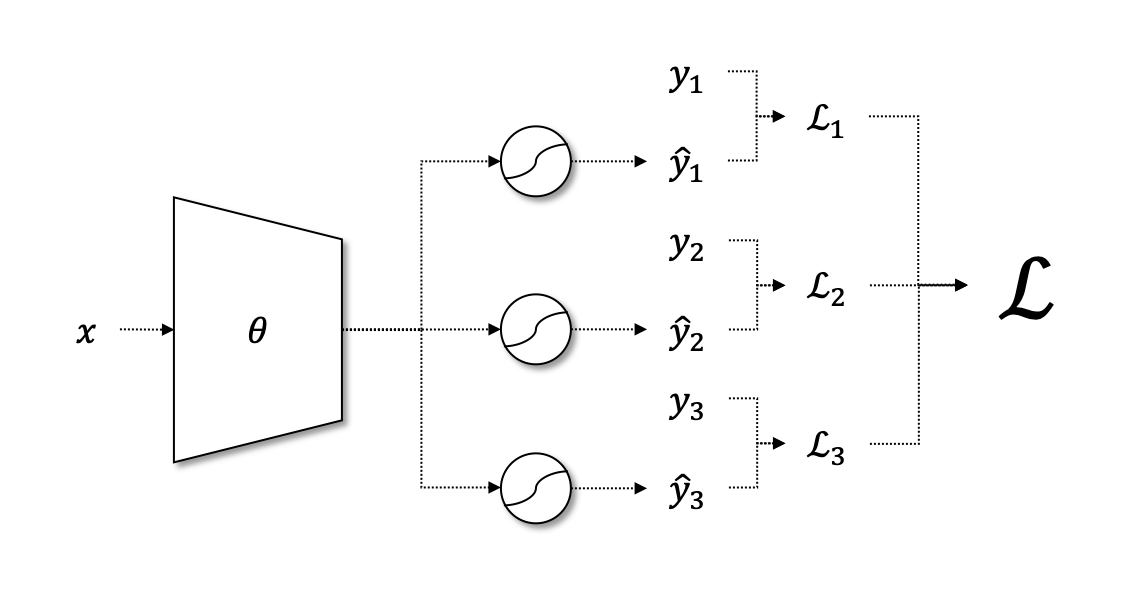
- 최종 손실 함수
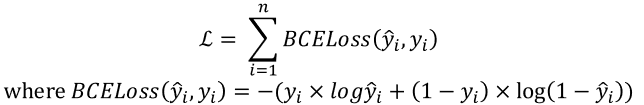
8.5.3. 이진 분류가 아닌 경우
: 분류하고자 하는 문제가 이진 분류가 아니라 다중 분류 일경우에는 softmax 계층이 필요함.
- 이진 분류가 아닌 예시 : 상 / 하 뿐만아니라 중 도 필요하다

위의 예시처럼 3개의 레이블이 존재하면 3개의 노드를 가지고, n개의 레이블이 존재하면 n개의 노드를 갖는 계층이 필요하다. 서로 다른 레이블에 대해 각각 분류를 해야하기 때문에, n개에 대해서 softmax계층이 적용된다.

- 최종 손실 함수

8.6. 마무리
: 예전에는 나이브 베이즈를 이용하여 분류를 시도하였으나, 요즘은 RNN/CNN과 같은 딥러닝 모델로 분류한다.
RNN은 순차 데이터를 받아 마지막 TIME-STEP에서 분류하여 문장 전체의 맥락과 의미에 대해 집중하여 분리한다.
CNN은 단어들의 조합에 대한 패턴을 감지하여 단어 조합에 대한 패턴의 유무를 가장 중요하게 집중하며 분리한다.
-> 이러한 각각의 장점을 조합하여 앙상블 모델로 구현하면 더 좋은 성능을 기대할 수도있다.
** 본 게시글은 아래 자연어 책을 공부하면서 작성하였습니다.
출처 : 김기현의 자연어 처리 딥러닝 캠프 _ 파이 토치 편
** 책에서 간단하게 넘어간 내용은, 아래 글들을 참고함
베이즈 정리 : angeloyeo.github.io/2020/01/09/Bayes_rule.html
딥러닝을 활용한 텍스트 분류 : wikidocs.net/24873




