| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- GRU
- Statistics
- 카이제곱분포
- 논문리뷰
- inner join
- MySQL
- 자연어 논문
- airflow
- torch
- NLP
- update
- 자연어 논문 리뷰
- LSTM
- SQL코테
- 서브쿼리
- HackerRank
- 그룹바이
- 코딩테스트
- sql
- t분포
- 짝수
- 표준편차
- 자연어처리
- leetcode
- CASE
- nlp논문
- SQL 날짜 데이터
- Window Function
- sigmoid
- 설명의무
- Today
- Total
HAZEL
[ NLP : CH7. 시퀀스 모델링 ] 순환 신경망, feedforward RNN, BPTT , Multi - Layer RNN,양방향 RNN ,LSTM, GRU, 그래디언트 클리핑 본문
[ NLP : CH7. 시퀀스 모델링 ] 순환 신경망, feedforward RNN, BPTT , Multi - Layer RNN,양방향 RNN ,LSTM, GRU, 그래디언트 클리핑
Rmsid01 2021. 1. 19. 16:037장 시퀀스 모델링 부분은 예전에 DL을 공부하고 정리한 파트와 유사함.
2020/12/21 - [DATA/ML & DL] - [Deep Learning 02 ] LSTM ( Long Short - Term Memory )
2020/12/26 - [DATA/ML & DL] - [Deep Learning 03 ] GRU ( Gated Recurrent Unit )
7장. 시퀀스 모델링
시퀀스 모델링 ( sequential modeling ) : 시간 개념 또는 순서 정보를 사용하여 입력을 학습하는 것. 신경망에서는 순환신경망 ( RNN ) 아키텍처를 통해 문제를 해결할 수 있음
7.1. 순환 신경망 ( RNN )
기존의 신경망 구조 : 정해진 입력 x를 받아 y를 출력해주는 형태 -> y= f( x: θ )
순환 신경망 ( RNN ) : 입력 x_t과 직전의 은닉 상태인 h_t-1 를 참조하여 현재의 상태인 h_t를 결정하는 작업을 여러 time-step에 걸쳐서 수행. 각 time-step별 RNN의 은닉상태는 경우에 따라 출력값이 될 수 있다. -> h_t= f(x_t, h_t-1 : θ)

7.1.1. 피드포워드 ( feedforward ; 순방향 )
: 출력으로 h_n 을 반환할 때 이렇게 얻어낸 h_t들을 y ̂_i로 삼아서 정답인 y_t와 비교하여 손실 L 을 계산함
: 기본적인 RNN의 피드 포어드 형태는 매 time-step마다 은닉 상태를 활용해 손실값을 계산할 수 있음.
1] RNN 과정
1) 각 입력과 출력 그리고 내부 파라미터의 크기


2) 입력 x_t를 받아서 입력에 대한 가중치 W를 곱하고 b를 더해준 후, 이전 time-step의 은닉 상태 에서의 값도 곱하고 더해준다. 이후에 활성화 함수 tanh를 거쳐 현재 time-step 은닉상태 h_t를 반환하게 된다.
[ ANN에서 이전 hidden states의 값들을 받아서 곱해주고 더해준 것이라고 생각하면 편하다. ]
RNN에서는 tanh를 주로 사용한다.


3) time-step별 y_t를 계산하여 다음 수식처럼 모든 time-step에 대한 손실 L을 구한후, time-step의 수만큼 평균을 냄

2] RNN의 입력 텐서와 은닉 상태 텐서의 크기
: 미니 배치까지 감안한 크기는 아래와 같다. 수식에서는 벡터로 표현되었지만, 현재 미니 배치 단위로 피드포워드 및 학습을 진행하고 있으므로, 벡터 대신 미니배치 내부의 샘플 인덱스 차원이 추가된 텐서가 실제 구현에서 사용된다.

- batch sixe ( 차원 배치 크기 ) : 미니 배치에서의 샘플 인덱스
- input size ( 차원 입력 크기 ) : 미리 정해진 입력 벡터의 차원 ( 임베딩 계층의 출력 벡터의 차원의 수)
- n : 현재 time-step의 인덱스를 나타냄. -> 위의 수식에서는 하나의 time - step 이므로 1을 적음.
-> n 개의 time-step을 가진 전체 시퀀스를 텐서로 나타내면 아래 그림이 됨


- hidden states 의 텐서의 크기를 n개의 time-step에 이어붙이면, RNN의 전체 time-step에 대한 출력 텐서가 됨.


7.1.2. BPTT ( Back propagation through time : 시간 축에 대해서 수행되는 역전파 방법 )
: 피드포워드를 통해서 구한 손실 L에 미분을 통해 역전파를 수행하게 되면, 각 time-step별로 뒤로 부터 θ의 기울기(gradient)가 구해지고, 이전 time-step(t-1)θ의 기울기에 더해짐. 즉, t가 0에 가까워질수록 RNN파라미터 θ의 기울기는 time-step별 기울기가 더해져 점점 커진다.

( ∂ : 편미분을 의미함 )

: 위의 그림처럼, RNN 역전파 속성으로 인해, time -step 수만큼 계층이 존재하는것과 동일한 상태가 된다.
즉, time-step이 길어지면, 매우 깊은 신경망과 유사하게 동작하기 된다. 이로 인해 기울기 소실 문제가 발생한다.
: 기울기 소실 문제가 발생하는 이유는, 활성화 함수로 tanh함수를 사용하기 때문이다.
RNN은 활성화함수로 tanh를 사용하는데, 이 함수의 도함수는 모두 기울기 값이 1보다 작거나 같다.
이로인해, 층을 거칠수록 기울기의 크기는 작아질 수 밖에 없다. [ 이 문제는 sigmoid 도 마찬가지다. ]
< 활성화 함수에 대한 내용은 나중에 한번 정리해서 포스팅 할 예정이다 >
-> 이로 인해, RNN 뿐만 아니라, 다층 퍼셉트론(Multilayer perceptrop : MLP ) 의 경우에도 기울기 소실문제가 발생한다. 하지만, 요즘 ReLU와 레지듀얼 커넥션의 등장으로 기울기 소실문제를 줄였다.
7.1.3. 다중 계층 순환 신경망 ( Multi - Layer RNN )

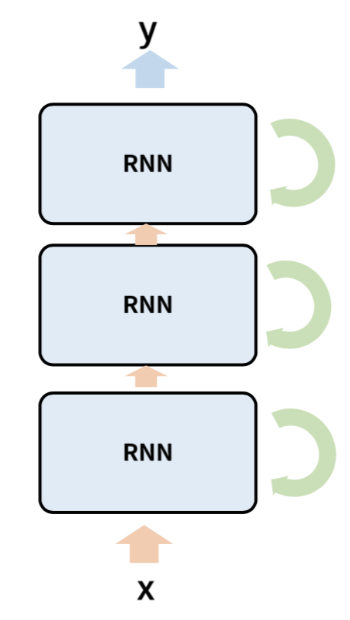
: 여러층의 RNN을 쌓아 올릴 수 있다.
: 시간의 흐름이 왼쪽에서 오른쪽 방향이라면, 여러 층을 아래에서 위로 쌓아 올리는 것을 말한다.
* multi - layer RNN 특징
1. 여러개의 RNN층이 쌓여 하나의 RNN을 이룰 때 가장 위층의 은닉 상태가 전체 RNN의 출력값이 된다.
( 위의 이미지는.. 내가 만들었지만, 직관적이지는 못한 것같다. )
2. 층별로 파라미터 θ를 공유하지 않고 따로 가짐. 보통 각 층 사이에 Dropout을 끼어 넣기도 함.
3. 각 Time -step의 rnn 전체 출력값은 맨 위측 hidden state 가 됨. ( 단일 RNN은 각 time-step은 은닉 상태와 출력값이 같은 값임 )
4. 하지만, RNN의 출력 텐서의 크기는 Vanilla RNN ( 단일, 1층 RNN) 과 동일하며,
출력 크기와 은닉 상태 크기는 아래와 같다.


7.1.4. 양방향 RNN ( Bi - directional RNN )
정방향 RNN : 기존에 말한 RNN으로, 시간을 1 부터 N까지 차례대로 입력받아 진행하는 것
양방향 RNN : 정방향 + 역방향( N부터 1까지 역방향으로 입력을 받아 진행하는 것 )
- 정방향과 역방향의 파라미터 θ는 공유되지 않음.
: 여러 층(multi - layer RNN ) 이면, 각 층마다 두방향의 time-step별 은닉 상태 값을 이어붙여 다음 층의 방향별 입력으로 사용한다. 경우에 따라서 전체 RNN층 가운데 일부만 양방향 RNN을 사용하기도 함.

7.1.5. 자연어 처리에 RNN 적용 사례

: 위의 사진 처럼, 타입별( 적용 사례 별로) 출력의 갯수가 다르기 때문에, RNN형태가 조금씩 다르다.
1. 하나의 출력을 사용할 경우,
: 하나의 출력을 사용한다는 것은, 보통 텍스트 분류에서 많이 사용된다. 이 경우, 단어(토큰)의 갯수만큼 입력이 들어가고, 마지막 time-step에서 softmax함수를 사용하여 클래스를 예측하는 확률 분포를 근사하도록 동작한다. RNN은 모든 time-step에 대해 출력을 반환하지만, 단일 출력에서는 마지막에서만 값을 반환한다.
- 일반적인 과정
: 단어를 원핫 벡터로 표현 -> 임베딩 계층을 거쳐 덴스벡터로 표현 -> RNN 입풋 data로 넣어줌.
-> RNN을 거쳐 출력값은 softmax함수를 넣어 멀티눌리 확률 분포로 값을 표현해줌. ( y^)
-> 원래 값도 원핫벡터로 되어 ( y ) 예측하려는 출려값 (y^) 과 교차 엔트로피 손실함수를 통해 손실값을 구한다.
2. 모든 출력을 사용할 경우
: 과정은 하나의 출력을 사용할 경우와 동일하지만, 여기서는 마지막 time-step 이 아닌, 모든 time-step별로 결과물을 출력하여, time-step별로 softmax함수를 취하는 점이 다르다.
- 대부분의 경우 bi - rnn이 가능하지만, 입출력이 서로 같은 데이터를 공유하면 양방향 RNN은 사용불가하다. 즉, 이전 time-step 출력값이 현재 time-step의 입력으로 쓰이는 모델은 안된다는 것을 의미한다. 이런 모델을 자기회귀 모델 ( Autoregressive Model : AR ; 이전 자신의 상태가 현재 자신의 상태를 결정하는 모델 ) 이라고 한다.
< 이렇게, Vanilla RNN에 대해서 다양하게 보았다. 이러한 RNN은 시간의 Step이 길어질수록 앞의 데이터를 기억하지못하는 단점이 존재한다. 이러한 문제를 해결하기 위해, LSTM과 GRU 아키텍처가 등장하였다 >
7.2. LSTM ( Long - Short term memory )
2020/12/21 - [DATA/ML & DL] - [Deep Learning 02 ] LSTM ( Long Short - Term Memory )
: 기존 RNN의 hidden state 뿐만 아니라, cell state 로 이전 기억을 도와준다. 뿐만 아니라, 다양한 gate를 이용하면서, 데이터를 기억하는데 더 효율적으로 대처할 수 있다. 즉, 장기 기억력에 더 나은 성능을 보인다.
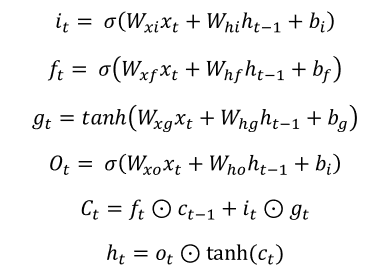
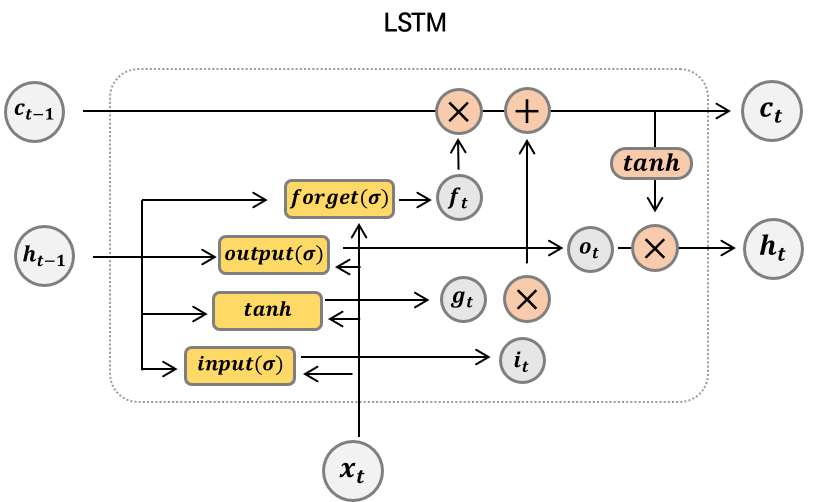
: 각 게이트를 시그모이드(sigmoid)함수를 이용하여, 0과 1 사이의 값으로 게이트를 얼마나 열고 닫을지 결정한다. 그 결정된 값에 따라서, cell state가 새롭게 인코딩된다.
: LSTM 또한, 다중 계층 LSTM , Bi-LSTM 이 가능하다.
7.3. GRU ( Gated recurrent unit )
2020/12/26 - [DATA/ML & DL] - [Deep Learning 03 ] GRU ( Gated Recurrent Unit )
: GRU는 LSTM의 간소화 버전이다.
: GRU는 Cell State가 없고, Hidden State만 존재하는 구조이다.
: Forget Gate 와 Input Gate가 결합되어있다.
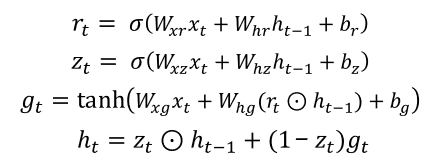
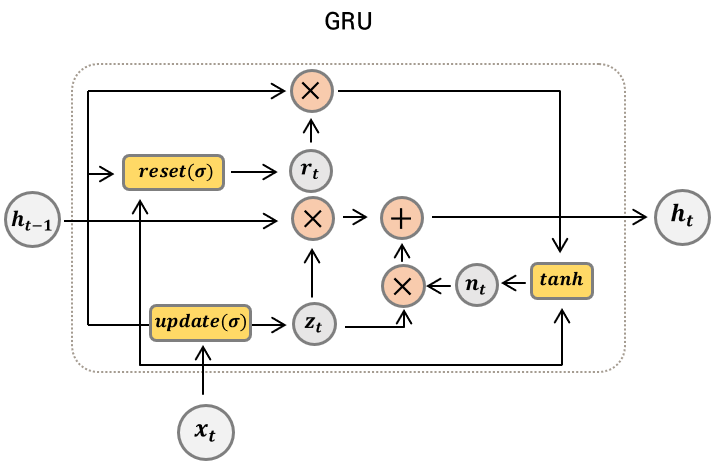
: LSTM에 비해 가벼운 몸집이지만, LSTM의 학습률이나 은닉상태 크기 등의 하이퍼 파라미터가 다르기 때문에, 사용 모델에 따라 파라미터 셋팅을 다시 찾아내야한다. 지금까지는 GRU 보다는 LSTM의 사용 빈도가 더 크다.
7.4. 그래디언트 클리핑 ( gradient clipping )
: RNN은 time-step마다 RNN 파라미터에 기울기가 더해지므로, 입력의 길이에 따라 기울기의 크기가 달라진다. 입력 길이가 너무 길면, 기울기가 커질 수 있으므로 학습률을 조절하여 경사하강법의 업데이트 속도를 조절해야한다.
[ 학습률 learning rate 는 너무 크면, 이동하는 크기가 너무 켜저, 학습을 제대로 못할 수도 있다. 만약 너무 작다면, 정확한 값으로 찾아갈 수는 있지만, 훈련 속도가 매우 느려지는 문제가 발생한다. ]
: 알맞은 값을 찾아 조절하기 위해 그래디언트 클라이핑 을 사용한다.
그래디언트 클리핑이란,
: 신경망 파라미터 θ의 norm( 보통 L2 norm)을 구하고, 이 norm의 크기를 제한하는 방법이다. 기울기 벡터 ( gradient vecor)의 방향은 유지하되, 학습이 무너지지 않을정도만 학습 크기를 줄일 수 있다. 이 norm의 최댓값은 하이퍼파라미터이다.
; 최댓값보다 큰 norm을 가진 기울기 벡터의 경우에만 그래디언트 클리핑을 수행하기 때문에, 능동적으로 학습을 조절하는 것과 비슷한 효과를 가진다.

: 기울기 norm 이 정해진 최댓값(역치, threshold )보다 크다면, 기울기 벡터를 최댓값보다 큰 만큼의 비율로 나누어짐. 따라서 기울기는 항상 역치보다 같거나 작아진다. 이를 통해, 기울이는 감소하지만 학습 방향을 잃지 않도록 한다. 즉, 손실 함수를 최소화 하기 위한 기울기의 방향은 유지한 상태로 크기만 줄어들게 되는 것이다. 하지만, 기존의 확률적 경사하강법 (SGD)가 아닌, Adam과 같은 동적인 학습률을 가지는 옵티마이저(optimizer)를 사용하면, 그래디언트 클리핑을 적용하지 않아도 상관없다. ( 김기현의 자연어 처리 딥러닝 캠프의 저자는 그럼에도 불구하고 안전장치로 적용하는 것은 괜찮은 생각이라고 표현함 )

import torch.optim as optim
import torch.nn.utils as torch_utils
learning_rate = 1.
max_grad_norm = 5.
optimizer = optim.SGD(model.parameters(), lr=learning_rate)
# In orther to avoid gradient exploding, we apply gradient clipping.
torch_utils.clip_grad_norm_(model.parameters(),
max_grad_norm
)
# Take a step of gradient descent.
optimizer.step()출처 : 김기현의 자연어 처리 딥러닝 캠프 _ 파이 토치 편
** 책에서 간단하게 넘어간 내용은, 아래 글들을 참고함
베이즈 정리 : angeloyeo.github.io/2020/01/09/Bayes_rule.html
딥러닝을 활용한 텍스트 분류 : wikidocs.net/24873
'DATA ANALYSIS > NLP' 카테고리의 다른 글
| [ NLP : CH10. 기계 번역 ] seq2seq, attention , Input Feeding (0) | 2021.02.17 |
|---|---|
| [ NLP : CH8. 텍스트 분류 ] 나이브베이즈, 베이즈정리, RNN/ CNN으로 텍스트 분류(1D 합성곱),멀티 레이블 분류 (0) | 2021.01.19 |
| [ NLP : CH6. 단어 임베딩 ] 차원축소, 주성분 분석, 매니폴드 가설, word2vec, Glove (0) | 2021.01.14 |
| [ NLP : CH5. 유사성과 모호성 ] 특징 벡터, 벡터 유사도, 단어 중의성, 선택 선호도 (0) | 2021.01.04 |
| [ NLP : CH5. 유사성과 모호성 ] 단어의 의미, 원핫 인코딩, 시소러스, 특징, TF-IDF (0) | 2020.12.27 |




