| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- leetcode
- 그룹바이
- torch
- 서브쿼리
- sql
- 코딩테스트
- nlp논문
- update
- sigmoid
- HackerRank
- LSTM
- MySQL
- 논문리뷰
- NLP
- CASE
- t분포
- Statistics
- 짝수
- SQL 날짜 데이터
- 자연어 논문
- airflow
- inner join
- 표준편차
- 설명의무
- GRU
- SQL코테
- 카이제곱분포
- Window Function
- 자연어처리
- 자연어 논문 리뷰
- Today
- Total
HAZEL
[ NLP : CH5. 유사성과 모호성 ] 특징 벡터, 벡터 유사도, 단어 중의성, 선택 선호도 본문
5장. 유사성과 모호성
5-6 . 특징 벡터 만들기
5.6.1. TF 행렬 만들기
TF : 단어의 문서별 출현 횟수

-> 공부의 특징 벡터 : [0,0,1]
한계점
- 문서가 적으면, 특징 벡터를 구성했다고 하기엔 무리가 존재함. 그러나 너무 많으면 지나치게 많은 차원이 생김
- 희소벡터가 될 수 있음 ( 벡터의 극히 일부분만 의미있는 값, 나머지는 0으로 채워진 벡터 ) -> 특정 통계를 얻는데 걸림돌 이 될 수 있음
5.6.2. 컨텍스트 윈도우로 함께 출현한 단어들의 정보 활용 ( Based on Context Window ( Co- occurrence ) )
- 윈도우 기반 동시 등장 행렬
- 단어별로 윈도우 내에 속해 있는 이웃 단어들의 출현 빈도를 세어 행렬로 나타내는 것
- window size 는 하이퍼파라미터 임. 너무 큰 크기를 가지면 현재 단어와 관계가 없는 단어들의 출현 빈도를 셈.
따라서 적절한 크기를 설정해야함.

한계점
- 동시 출현 빈도가 높은 빈도들은 괜찮지만, 동시 출현 빈도가 낮은 단어들은 0으로 채워져 희소성 문제가 발생함
- 이러한 희소벡터들이 많으면, 유사도를 구하거나 벡터간 연산을 할 때, 직교하는 경우가 많아 곤란함
5-7. 벡터 유사도 구하기
5.7.1. L1 거리
: L1 거리란, L1 norm 을 사용한 것으로 맨해튼 거리( Manhattan distance)라고 함.
: 두 벡터의 각 차원별 값의 차이의 절대값을 모두 합한 값

import torch
def get_l1_distance(x1, x2):
return ( (x1 - x2 ).abs()).sum()5.7.2. L2 거리
: L2 거리란, 유클리디안 거리 이다.
: 차원별 값 차이의 제곱의 합에 루트를 취한 형태이다.

def get_l2_distance(x1, x2 ) :
return ((x1 - x2)**2).sum()**.5
5.7.3. infinity Norm
: 차원 별 값의 차이 중 가장 큰 값을 나타냄

def get_infinity_distance(x1, x2):
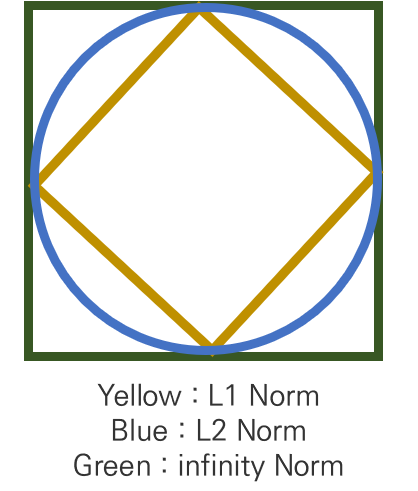
return ((x1 - x2).abs()).max()5.7.4. L1 , L2, infinity norm 비교
: L1 거리는 각 값들을 동시에 나타냄 < 원소들의 차이 (거리)를 제일 많이 반영한다 라는 느낌 .>
- 하지만, L2 와 infinity Norm 으로 갈 수록 벡터 내의 큰 값에 더욱 집중해서 거리를 나타냄.
: 각 거리를 최소화 하도록 최적화 수행한다면 L2, infinity Norm 로 갈수록 전체 벡터 중에서 큰 값이 작아지도록 최적화 수행을 함
5.7.5. 코사인 유사도
: 두 벡터 사이의 방향과 크기를 모두 고려하는 방법 ( 각도 기반 유사도 측정 )

- 분수의 윗변은 Dot product : 두 벡터 사이의 요소별 곱을 사용 = 벡터의 내적 이다.
- 코사인 유사도 결과가 1에 가까울수록 방향은 일치 , 0에 가까울수록 직교이며, -1 에 가까울수록 반대방향이다.
- 크기와 방향을 모두 고려하는, 자연어 처리에서 널리 쓰이는 자연어 처리 방법이다.
- 장점 : 크기와 방향을 모두 고려하는 방법임
- 단점 : 연산이 비쌈 - 윗변의 벡터 내적연산, 밑변의 벡터 크기 연산은 비쌈 따라서, 벡터 차원의 크기가 클수록 연산량이 부담이 생김
- 특히, 희소 벡터일경우 0이 들어간 차원이 많이면, 해당 차원이 직교하면서 곱의 값이 0이 되므로, 정확한 유사도 또는 거리를 반영하지 못함.
def get_cosine_similarity ( x1, x2 ):
return (x1 * x2).sum() / ((x1**2).sum()**.5 * (x2**2).sum()**.5)
5.7.6. 자카드 유사도 ( jaccard similarity )
: 두 집합 간의 유사도를 구하는 방법

- 수식의 윗변 : 두 집합의 교집합 크기
- 수식의 밑변 : 두 집합의 합집합 크기로 나누어줌
- 특징 벡터의 각 차원 : 집합의 요소
: 단, 차원에서의 값이 0 또는 0이 아닌 값이 아니라 수치 자체에 대해 자카드 유사도를 구하고자 할 때, 두 벡터의 각 차원의 숫자에 대해 min, max 연산을 통해서 계산할 수 있다.
def get_faccard_similarity ( x1, x2 ):
return torch.stack([x1 , x2]).min(dim=0)[0].sum() / torch.stack([x1, x2 ])
# torch.stack 는 두개의 텐서를 결합하는 함수이다.
5.7.7. 문서간의 유사도 구하기
: 위의 내용은 다, 단어간의 유사도를 구한 것. 이처럼 문서에 대한 특징을 추출해서 유사도 구할 수 있음
예를 들어, 문서내 단어들에 대한 TF나 TF-IDF를 구하여 벡터를 구성하고, 이를 활용하여 벡터 사이의 유사도를 구할 수도있다. ( 하지만, 요즘은 딥러닝으로 더 나은 문서간 유사도를 구할 수 있다 )
5-8. 단어 중의성 해소
5.8.1. 시소러스 기반 중의성 해소 : 레스크 알고리즘 ( Lesk algorithm )
: 간단한 사전 기반 중의성 해소 방법
: 주어진 문장에서 특정 단어의 의미를 명확히 할 때 사용할 수 있음
: 레스크 알고리즘의 가정 - 문장 내에 같이 등장하는 단어들은 공통 토픽을 공유한다는 것
- 레스크 알고리즘 개요
1. 중의성을 해소하고자 하는 단어에 대해 사전 ( 주로 워드넷 )의 의미별 설명을 구함
2. 주어진 문장 내에 등장한 단어의 사전에서 의미별 설명 사이의 유사도를 구함
- 유사도 구하는 방법은 여러가지 중, 겹치는 단어의 개수를 구하는 것이 존재.
3. 문장 내 단어들의 의미별 설명과 가장 유사도가 높은 의미를 선택
def lesk(sentence, word):
from nltk.wsd import lesk
best_synset = lesk(sentence.split(), word)
print(best_synset, best_synset.definition())
- 레스크 알고리즘의 장단점
: 장점 - 워드넷 같이 잘 분류된 사전이 있다면, 쉽고 빠르게 중의성 해소 문제를 해결 할 수 있음
- 이미 단어별로 몇개의 의미를 지니는지 잘 정의해 두었기에 크게 고민할 필요 없음
: 단점 - 사전의 단어 및 의미에 관한 설명에 크게 의존
- 설명이 부실하거나 주어진 문장에 큰 특징이 없을 경우, 단어 중의성 해소 능력이 떨어짐
- 사전이 존재하지 않는 언어에 대해서는 레스크 알고리즘 자체의 수행이 어려움
5-9. 선택 선호도
5.9.1. 선택 선호도 강도
선택 선호도란, : 단어와 단어 사이의 관계가 좀 더 특별한 경우를 수치화하여 나타냄
- 술어 동사가 주어졌을 때, 목적어 관계에 있는 표제어 단어들의 분포는 평소 문서 내에 해당 명사가 나올 분포와 다를 것
- 그 분포의 차이가 크면 클 수록, 해당 술어는 더 강력한 선택 선호도를 갖는다.
- 필립 레스닉 "선택 선호도 강도 라고 명명하고 쿨백-라이블러발산(KLD)을 사용하여 정의했다 "
*** 쿨백-라이블러 발산(KLD)은 두 확률분포의 차이를 계산하는데 사용하는 함수로, 어떤 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면, 발생할 수 있는 정보 엔트로피 차이를 계산한다. 상대 엔트로피, 정보획득량 , 인포메이션 다이버전스 라고도 함. 출처 : ko.wikipedia.org/wiki/%EC%BF%A8%EB%B0%B1-%EB%9D%BC%EC%9D%B4%EB%B8%94%EB%9F%AC_%EB%B0%9C%EC%82%B0

: 선택 선호도 강도 S_r(w)은 w가 주어졌을 때의 오브젝트 클래스 c의 분포 P(C|w)와, 그냥 해당 클래스의 사전 분포 P(C)와의 KLD로 정의되어있다
: 즉, 선택 선호도 강도는 술어가 표제어로 특정 클래스를 얼마나 선택적으로 선호하는지에 대한 수치라고 할 수있음.
5.9.2. 선택 관련도
: 술어와 특정 클래스 사이의 선택 관련도 ( Selectional association )

- 선택 선호도가 강도가 낮은 술어에 대해 윕변의 값이 큰경우에는 술어와 클래스 사이에 더 큰 선택 관련도를 갖는다고 정의함.
- 즉, 선택 선호도 강도가 낮아서, 해당 술어는 클래스에 대한 선택적 선호 강도가 낮음에도 불구하고, 특정 클래스만 유독 술어에 영향을 받아서 윗변이 커질수록 선택 관련도의 수치도 커짐
5.9.3. 유사도 기반의 선택 선호도
: 단어간 유사도를 통해 시소로스에 의존하지 않고 데이터를 기반으로 간단하게 선택 선호도를 구하는 방법을 제시함 ( 카트린 어크 )

- 술어 : w, 표제어 : h, 두 단어 사이의 관계 R이 튜플로 주어짐
- Sim 함수는 이전에 다룬 다양한 유사도 함수를 사용할 수 있음
- 이전에 다루었던 선택 관련도는 A_R(w,c) 을 다루었는데, 지금은 A_R(w, h_0)을 다루는 것이 차이점
- 장점 : 워드넷과 같은 시소러스 없이도 쉽게 선호도를 계산할 수 있게 함, 많은 코퍼스를 가지고있고, 정확한 특징 벡터를 구상할수록 정확한 유사도 계산이 가능해져 점점 더 좋은 성능의 중의성 해소가 가능함.
- 단점 : 유사도를 비교하기 위해서 Seen_r(W) 함수를 통헤 대상을 선정하기 때문에, 코퍼스에 따라 유사도를 구할 수 있는 대상이 달라짐. 그에 따라 커버리지 문제가 발생할 수 있음
- 구현해 보면 보다라는 동사에 대한 유사도를 알 수 있다.

5.9.4. 결론
- 5장에서 배운 전통적인 자연어 처리에서는 희소성 문제를 가진다.
하지만, 요즘은 딥러닝에서는 단어의 특징 벡터를 희소벡터로 만들기 보다는 임베딩 기법을 통해 0 이 잘 존재하지 않는 덴스(dense) 벡터로 만들어 사용한다.
** 본 게시글은 아래 자연어 책을 공부하면서 작성하였습니다.
출처 : 김기현의 자연어 처리 딥러닝 캠프 _ 파이 토치 편
web.stanford.edu/class/cs224n/readings/cs224n-2019-notes01-wordvecs1.pdf




