| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Statistics
- inner join
- nlp논문
- 서브쿼리
- GRU
- 자연어처리
- leetcode
- Window Function
- NLP
- 짝수
- torch
- 카이제곱분포
- CASE
- 설명의무
- HackerRank
- airflow
- LSTM
- 자연어 논문 리뷰
- SQL코테
- MySQL
- t분포
- 그룹바이
- 코딩테스트
- 표준편차
- 자연어 논문
- update
- sigmoid
- SQL 날짜 데이터
- 논문리뷰
- sql
- Today
- Total
HAZEL
[Basic Statistics : CH 6. 가설검정] 가설검정과 유의 수준 , 모집단 평균의 가설검정, 모집단 비율 및 분산의 가설 검정 본문
[Basic Statistics : CH 6. 가설검정] 가설검정과 유의 수준 , 모집단 평균의 가설검정, 모집단 비율 및 분산의 가설 검정
Rmsid01 2020. 12. 2. 11:33CH6. 가설검정 ( Hypothesis Testing )
01 . 가설검정과 유의수준
001. 가설
- 주어진 사실 혹은 조사하고자 하는 사실이 어떠하다는 주장이나 추측
' 모수는 어떠할 것이다 ! '
1. 귀무가설 ( null hypothesis ) [ 귀무 : 원점으로 돌아가다. 일반적으로 믿는 사실 ] = 영가설 = H0
: 조사를 할 필요가 없는, 연구를 할 필요가 없는 가설
: 귀무가설이 아니라는 충분한 증거를 데이터로부터 보임으로써 대립가설을 입증.
: 귀무가설 하에서 통계량의 분포를 아는 것이 검정의 핵심
2. 대립가설 ( anti - hypothesis ) = H1
: 귀무가설(영가설)에 대립하는 가설 , 연구를 위한 가설 , 입증하여 주장하고자하는 가설
002. 검정 ( TESTING )
- 검정 : 주어진 사실 혹은 조사하고자 하는 사실이 어떠하다는 주장이나 추측
유의수준 ( α ) 를 세워두고, 유의수준 안에 포함되면 기각하고 포함되지 않으면 채택함.
1. 양측 검정 ( Two-sided test )
: α가 양쪽에 있는 것
: 조사하고자 하는 대립가설, 즉, '사실이 아니다'라는 것을 검정하여 귀무가설을 기각하고 대립가설을 채택하고자 하는 것
: 기준점을 기준으로 적은것, 많은 것 사이인 1-α에 해당하면 채택하는 것.

2. 단측 검정 ( one - sided test )
: α가 한쪽에만 있는 것
: 조사의 목적에 따라 대립가설을 x 값보다 적다고 수립하거나, 혹은 x값보다 많다고 수립하여 한 쪽만 살펴보는 것
: 어떤 값 아래 혹은 위로 가면 귀무가설을 기각하는 것.

003. 통계적 판단
: 데이터를 기준으로 통계량을 계산했을 때 , 즉 모수를 추정 했을 때, 이것은 항상 틀릴 가능성을 내포한다.
통계학에서는 모수의 추정이 맞을지 틀릴지를 판단하는 것을 유의수준 ( α ) 라고 함.
1. 통계적 판단
- 틀릴 가능성 : α ( p ( 확률 ) 값 , p -value 라고 표현함 )
- 맞을 가능성 : 1 - α
2. 추정은 틀릴 가능성을 내포
- 오류 : 모수를 추정한 결과가 실제와는 다른 결론에 도달하는 것
- 1종 오류 ( type 1 error ) : 귀무가설을 채택해야하는 상황에서, 귀무가설을 채택하지 않고 기각하는 오류
: 귀무가설이 맞을 때 , 귀무가설을 기각하는 오류 - 1종 오류를 조금 더 조심히 다룸.
- 2종 오류 ( type 2 error ) : 귀무가설을 기각해야하는 상황에서, 귀무가설을 채택하는 오류
: 귀무가설이 틀렸을 때, 귀무가설을 기각하지 않는 오류

- 검정 통계량 : 표본에서 구해낼 수 있는 함수, 이 값을 기준으로 귀무가설 기각여부를 결정.
- 기각역 : 검정통계량이 취하는 구간 중 귀무가설을 기각하는 구간.
: 기각역은 적당하게 잡아야함 !!
-> 기각역을 크게 잡는다면 검정통계량이 모수의 값과 많이 떨어져 있지 않음에도 불구하고 H0이 기각하게 됨
= 많은경우의 대립가설을 채택하게 됨 = 1종오류를 범할 가능성이 높아짐 = 2종오류를 범할 가능성은 낮아짐.
-> 기각역이 줄어들면, 1종오류를 범할 확률은 낮아지고 2종오류를 범할 확률은 높아짐
004. 가설검검정의 검정력 ( power of hypothesis testing )
: 귀무가설을 채택해야하지만 귀무가설을 기각하는 경우의 확률은 ( 1종 오류) -> 유의수준 α로 표시
: 귀무가설을 기각해야 함에도 귀무가설을 채택하는 경우의 확률은 ( 2종 오류 ) -> β로 표시
- 2종오류가 발생하지 않을 확률 -> 1 - β
005. 가설을 통한 위사결정 과정
1. 가설 수립
: H0와 H1를 결정하는 것
2. 유의수준 결정
: H0을 채택할지 H1을 채택할지 기준을 마련하는데, 그 기준을 마련하는 것이 바로 유의수준을 결정
ex, 95%를 할지, 99%을 할지
3. 기각역 설정
: 분포가 있을 때, 양측 검정을 할지, 단측 검정을 할지 어떤 가설을 선택할지 판단.
4. 통계량 계산
: 기각역과 채택역 사이를 이루는 임계치를 기준으로 우리가 얻은 데이터를 통해 통계량 계산
임계치를 벗어나지 않으면 채택, 벗어나면 기각
5. 의사결정
02. 모집단 평균의 가설검정 ( 모분산을 아는 경우 )
001. 가설 수립
- 귀무가설 : 모평균이 계산된 특정 값과 동일

- 대립가설
1) 양측검정의 경우 모평균이 특정 값과 동일하지 않음

2) 단측검정의 경우에는
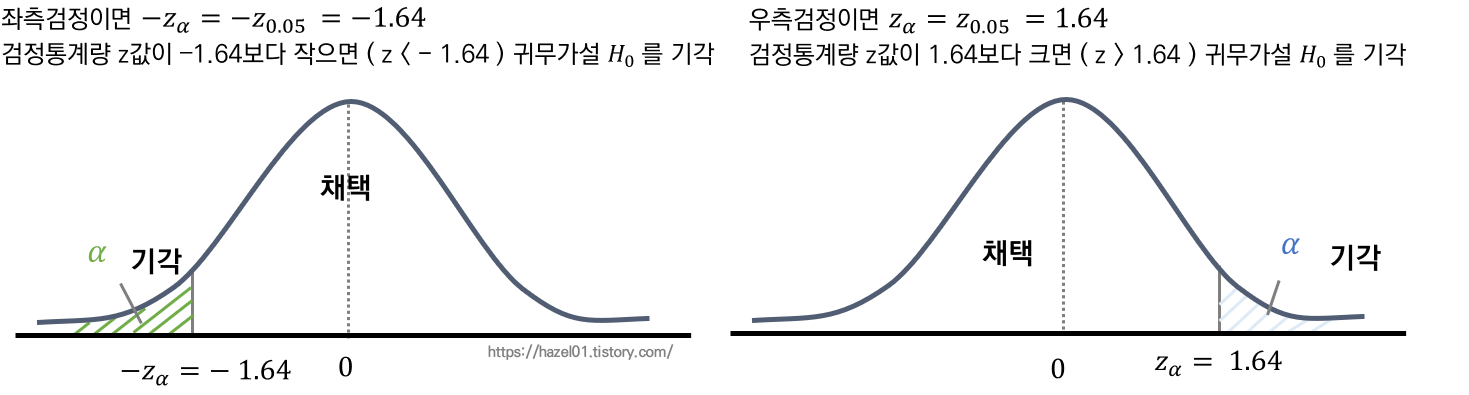
- 좌측 검정 :

- 우측 검정

002. 유의수준의 결정

- 예시
표본 300개, 특정값 = 300 ,평균 = 244.65 , 표준편차 20 , 유의수준 0.05에서의 좌측검정
: H0 : μ = 300 , H1 = μ < 300, α = 0.05 , n = 300 , 조사된 평균 = 244.65 , 표준편차 = 20
-z_0.05 = -1.64 , -z < - 1.64 보다 작다면 , H0 기각이됨. H1을 선택
Z = ( 244.65 - 300 ) / ( 20/ √300 ) = - 47.935
즉, Z < - 1.64 를 만족함. 즉 H0은 기각되고, H1가 채택됨. = 특정값은 300이 되지 않는다!
03. 모집단의 평균의 가설 검정 ( 모분산을 모르는 경우 ) [ 실전 ! 두둥 ! ]
** 표본이 크다 작다 의 판단은 중심극한정리에 근거해서 표본의 갯수 n = 30 을 기준으로 함.
30개를 넘어가면 Z 검정을 실시. 30개가 되지않으면 T 검정을 함.
하지만, T 분포도 표본이 많아지면 Z 분포에 근접하게 됨
001. 표본이 큰 경우의 가설 검정
- Z 통계량을 가짐. ~ N(0,1) 정규분포를 가짐
- 이 때 관측치의 수가 충분하다면 (30개 이상) 모집단의 표준편차 대신 표본의 표준편차로 대체 가능
- n이 무한대로 수렴한다면, 표본의 표준편차는 모집단의 표준 편차에 근접하다. -> 따라서, 모분산을 알 경우의 공식과 유사하다.

002. 표본이 작은 경우의 가설 검정
- t 분포를 가짐.
- z 검정과 t 검정의 차이는 : 자유도의 개념 , 자유도가 커질수록 정규분포에 근사

003. z검정과 t 검정의 관계
: 전체가 t검정, 일부분이 z검정

- 예시
표본 15개, 특정값 = 300 ,평균 = 302.1 , 표준편차 14.54 , 유의수준 0.05에서의 좌측검정 , 모집단의 분포는 정규분포라 가
: t 값 = 302.1 - 300 / ( 14.54 / √15 ) = 0.568 , n-1 = 14 , α = 0.05
( t분포 값은 -1.761 - t 분포표를 보면 확인 할 수 있음 )
좌측 검정이기 때문에, t < -1.761 이면 기각됨. 하지만, 위에서 구한 t 값은 0.568이기 때문에, 기각되지 않고 H0 채택!
즉, 특정값 300 이 맞다!
03. 모집단의 평균의 가설 검정 ( P값을 이용한 가설 검정 )
001. 지금까지의 방법
- 유의수준에 따라 채택/ 기각을 결정한 지금까지의 방법은 신뢰범위에 포함되는지 그렇지 않은지만 제시하므로 채택/기각에 대한 강도를 표현하기에는 충분하지 않음
002. P값을 이용한 가설 검정
- 유의확률 ( P-value )
: 주어진 검정통계량 값을 기준으로 해당 값보다 대립가설을 더 선호하는 검정통계량 값이 나올 확률
: 이 값이 유의 수준보다 낮으면 귀무가설을 기각. 즉, p 값 < α 이면, 기각
- P값은 귀무가설을 기각하기 위한 최대한의 한계점을 나타냄
- 유의수준 α를 기준으로 보면 α로부터 멀리 떨어져 있는 확률을 나타낸다.

- 전체가 100이기 때문에, P = 1 이다. 1을 기준으로 기각역이 우측에 있으면, 최소한 P가 0.05 보다 작거나 같다면, 귀무가설을 기각이 됨.
- 기각안에 들어갈 확률이 5%
- P값의 다른 표현 : P-value, significance level (혹은 sig. ), 유의 수준, 유의확률
- p값은 0에서 1안에 해당하는 값
- 예시
표본 300개, 특정값 = 300 ,평균 = 294.65 , 표준편차 45 , 유의수준 0.05에서 귀무가설의 기각여부를 판단하라.
: H0 : μ = 300 , H1 = μ < 300, α = 0.05 , n = 300 , 조사된 평균 = 294.65 , 표준편차 = 45
통계량 z = - 2.059 , p = P( z < -2.059 ) => 0.5 - [ 0 ≤ z ≤ 2.059 ] => 0.5 - 0.48 = 0.02

03. 모집단 비율 및 분산의 가설검정
001. 모집단 비율에 대한 가설검정 : 모집단에 대한 특성을 비율로 가늠하여 검정하는 것
ex, 전자제품의 AS 센터에서 100명의 고객이 서비스를 받았다고 할때, 과연 몇 %의 고객이 만족감을 느꼈을지 확인하는 조사
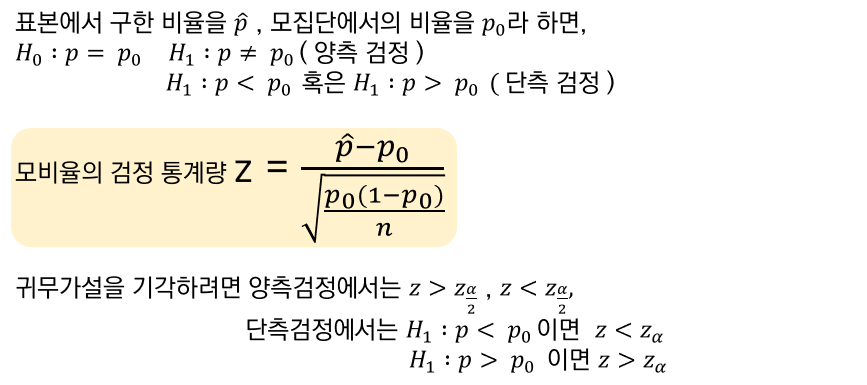
002. 모집단 분산에 대한 가설검정 : 평균에 대해 어느정도의 산포가 나타나는지를 살펴보는 가설검정
: 분산이 σ^2인 모집단으로부터 n개의 표본을 추출해서 표본분산 s^2을 계산 한다면 ?
- 자유도 = n -1 , 카이제곱 분포를 따르는 분포가 됨.

공부 교재 : 제대로 시작하는 기초통계학
사회조사분석사
https://www.youtube.com/watch?v=jGOqkljySu8&list=PLsri7w6p16vuDN55ZGHVYnitXs2R1Wz6q




