| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- t분포
- sql
- 서브쿼리
- Window Function
- MySQL
- 짝수
- 그룹바이
- leetcode
- 자연어 논문
- 논문리뷰
- inner join
- 표준편차
- torch
- NLP
- 자연어 논문 리뷰
- HackerRank
- CASE
- Statistics
- SQL코테
- SQL 날짜 데이터
- 코딩테스트
- nlp논문
- sigmoid
- LSTM
- update
- 자연어처리
- 카이제곱분포
- airflow
- 설명의무
- GRU
- Today
- Total
HAZEL
[ NLP : CH2. 기초수학 ] 확률변수와 확률 분포/ 기댓값과 샘플링 / MLE / 정보이론 본문
[ NLP : CH2. 기초수학 ] 확률변수와 확률 분포/ 기댓값과 샘플링 / MLE / 정보이론
Rmsid01 2020. 12. 17. 11:482장. 기초수학
2-1. 확률 변수와 확률 분포
2.1.1. 확률 변수
001. 랜덤 변수와 확률
- 랜덤 변수 : 랜덤 하게 발생하는 어떤 사건을 정의함

- 괄호 안의 확률 변수가 특정 값을 가질 때 확률 값을 반환하는 함수
- 확률 변수 x가 값 x가 나올 확률 값 p
- 이 때, 확률 p는 0에서 1 사이의 값이 될 수 있다.
- 확률 변수 x가 가질 수 있는 N개의 값에 대한 확률을 모두 더하면 1이 된다.
002. 이산확률 변수와 이산 확률 분포
- 이산 확률 분포 : 불연속적인 랜덤 변수를 다루는 것
- 확률 질량 함수 : 불연속적인 이산 확률 변수에 대한 확률 함수
EX, 베르누이 분포, 멀티 눌리 분포
- 베르누이 분포 : 0과 1 두 개의 값만 가질 수 있다.
-> 이항분포 : 확률 분포를 더 일반화하여 여러 번 일어날 수 있는 확률에 대해 이야기한 분포
- 멀티눌리 확률분포 : 주사위의 경우와 같이 여러 개의 이산적인 값을 가질 수 있다.
-> 다항 분포 : 확률 분포를 더 일반화하여 여러 번 일어날 수 있는 확률에 대해 이야기한 분포
003. 연속 확률 변수와 연속 확률 분포
- 연속 확률 변수 : 연속적인 값을 다루는 것
- 연속 확률 분포 ( 확률 밀도 함수) : 연속확률변수를 가지는 확률 분포
: 확률변수로 정의된 공간에 대해 확률값이 아닌 확률 밀도로 정의할 수 있다.

- 어떤 값에 대한 확률 밀도 p(x)은 꼭 1보다 작을 필요는 없으며, p(x)를 적분한 것은 항상 1이다.
ex, 정규분포 ( 가우시안 분포 )

2.1.2. 결합 확률
: 두개 이상의 사건이 동시에 일어날 확률 P ( A, B )
-> 따라서 두 개 이상의 확률 변수를 가짐
- 독립 : 발생하는 사건이 서로에게 영향을 끼치지 않는 것
: 두 사건이 서로 독립관계라면, P(A, B) = P(A) P(B)가 성립한다.
2.1.3. 조건부 확률
: 하나의 확률 변수가 주어졌을 때, 다른 확률 변수에 대한 확률 분포

ex, P(A|B =2) : B가 2가 나올 때, A 에서 얻을 수 있는 확률 분포. A값을 모르니까 때문에, 확률의 값을 반환하는 것이 아니라 확률 분포 함수를 반환한다.
베이즈 정리

2.1.4. 주변 확률 분포
: 두개 이상의 확률 변수의 결합 확률 분포가 있을 때, 하나의 확률 변수에 대해서 적분을 수행한 결과
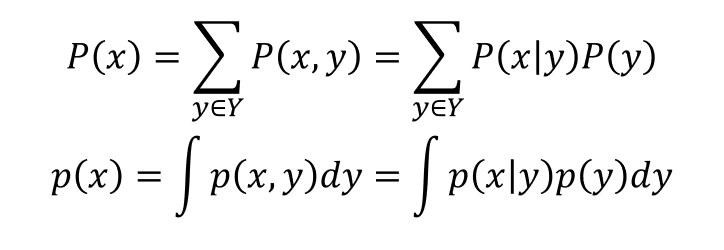
2-2. 기댓값과 샘플링
2.2.1. 기댓값
: 기댓값은 보상과 그 보상을 받을 확률을 곱한 값의 총합
: 즉, 보상에 대한 가중평균
- 주사위에 대한 예시를 수식으로 표현하기

- 주사위에 대한 예시는 연속확률변수는 아니지만, 만약, 연속 확률 변수라면 어떻게 공식을 세워야 하는지 적은 것이다.
2.2.2. 몬테카를로 샘플링
: 랜덤 성질을 이용하여 임의의 함수 적분을 근사하는 방법

2-3. 최대가능도 추정(MLE)
2.3.1. MLE
일반화 : 데이터를 잘 설명할 수 있거나, 주어진 데이터로부터 결괏값을 잘 예측하는 것들
- 가능도(우도) : 주어진 데이터 { x : a, b, c }를 설명하는 확률분포 파라미터(θ)에 대한 함수

: 따라서, 이산확률변수를 갖는 확률 분포에서는 확률 값 자체가 가능 도로 표현됨.
연속 확률 변수를 갖는 확률 분포의 경우에는 확률 밀도 값이 가능도를 나타냄.
ex, 서로 독립인 n번 시행을 거쳐 얻은 데이터( x1 , x2, x3 )에 대한 가능도는 아래처럼 표현 가능

- x|θ는 확률 밀도함수에서 x가 가지는 y. 즉 높이를 의미한다. 이 높이들을 다 곱해서 가장 커질 때, 값들이 이그래프를 잘 설명하고 있다고 말할 수 있게 되는 것이다.
위의 수식에 로그를 취하면, 곱을 합으로 표현할 수 있다. [ 로그 가능도 ]

로그로 취하면 좋은 점?!
1. 소수점이 너무 작게 표현되어 언더 플로 현상이 나는 것을 방지할 수 있다.
2. 곱셈 연산을 덧셈 연산으로 바꾸어주어 연산을 빠르게 할 수 있다.
3. 가우시안 분포(정규분포)에서 지수(exponent)를 제거할 수 있다.

: 가능도에 로그를 취하여 로그 가능도를 최대화할 수 있다. 이는 가능도를 최대화한 것과 같은 값을 가진다.
만약 -1을 곱하면 최소화 문제로 치환할 수 있다.
-1이 곱해진 로그 가능도를 음의 로그 가능도(negative log-likelihood , NLL)이라고 부른다.
즉, NLL 값을 최소화하면 MLE를 하는 것과 같은 효과를 얻을 수 있다.
2.3.2. 확률 분포 함수로서의 신경망
- 신경망도 확률 분포 함수다.
- 신경망 가중치 파라미터 θ가 훈련 데이터를 잘 설명하도록 경사 하강법(Gradient descent)을 통해 MLE를 수행하여 학습한다.
2-4. 정보이론
2.4.1. 정보량
- 정보이론 : 데이터를 정량화하기 위한 응용수학의 분야, 신경망과 밀접한 연관이 있다.
- 정보량 : 불확실성 또는 놀람의 정도 - 정보량이 높다는 것은 일어날 확률이 낮은 것을 의미함.
- 확률이 낮은 사건에 대한 정보가 맞으면 그 정보는 굉장히 소중해 짐

2.4.2. 엔트로피
엔트로피 : 정보량의 평균(기댓값)을 취할 수 있음
: 분포의 대략적인 모양이 얼마나 퍼져있는지, 뾰족한지 가늠할 수 있는 척도
> 엔트로피가 작으면 뾰족함. = 특정 값에 대한 확률이 높다.

교차 엔트로피 : 분포 함수 P에서 샘플링한 x 를 통해 분포함수 Q의 평균 정보량을 나타낸 것.
: 다른 분포 P를 사용하여 대상 분포 Q의 엔트로피를 측정함.

- 교차 엔트로피는 보통 이산 확률변수를 다루는 확률 분포에 해당하는 내용이다.
- 연속 확률 분포의 경우는 보통 평균 제곱 오차(MSE)를 사용하여 훈련한다.
2.4.3. 쿨백-라이블러 발산 ( Kullback-LeIbler divergence : KLD )
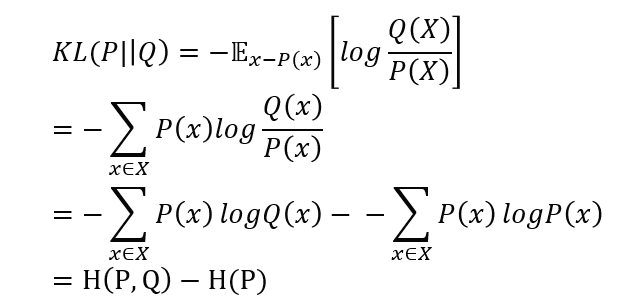
: KLD는 두 분포 사이의 괴리를 보여줌

: KLD를 미분하면 교차 엔트로피와 같은 미분 결괏값이 나온다.
즉, 교차 엔트로피를 손실 함수로 활용하여 경사 하강법을 수행하는 것과, KLD를 손실함수로 사용하여 경사하강법을 수행해 신경망을 훈련하는 것과 과정이 같다고 말할 수 있다.
** 본 게시글은 자연어 책을 공부하면서 정리한 것
출처 : 김기현의 자연어 처리 딥러닝 캠프 _ 파이 토치 편
ratsgo.github.io/statistics/2017/09/22/information/




